Н. И. Брунов. О пропорциях в архитектуре Древней Греции. 1936

Leo von Klenze: Reconstruction of the Acropolis and Areopagus in Athens. 1846. Source: commons.wikimedia.org

 

 

Статья искусствоведа и историка архитектуры Н. И. Брунова «О пропорциях в архитектуре Древней Греции» из сборника «Проблемы архитектуры : Сборник материалов : Том I, книга 1» (Москва : Издательство Всесоюзной Академии архитектуры, 1936).

 

Николай Иванович Брунов (1898—1971) — советский историк архитектуры, доктор искусствоведения (1943), член-корреспондент Академии архитектуры СССР (1940). Основной круг научных интересов — античная, византийская и древнерусская архитектура.

 

 

 

 

 

До сих пор распространена была так называемая модульная система, объясняющая пропорции классической греческой архитектуры. Но исследования последнего времени ее опровергли. Новейшие изыскания привели к заключению, что пропорции классических произведений построены на иррациональных числах, в то время как модульная система основана на простых целых числах. Согласно модульной системе в здании берется какая-нибудь его часть, по отношению к которой остальные размеры представляют собой кратные отношения, выражаемые в простых числах. Три новейших теории дают наиболее простые и убедительные решения античных пропорций. Их авторы: Жолтовский, Хэмбидж и Мёссель.

 

У Жолтовского был предшественник, теория которого очень важна. Это — Цейзинг, автор двух важных сочинений: «Neue Lehre über die Proportionen des menschlichen Körpers», 1854 г., и «Aesthetische Forschungen», 1855 г. Цейзинг сформулировал несколько основных положений, получивших широкое распространение и повторяемых многими авторами. Первое положение его утверждает, что золотое сечение господствует в природе; Цейзинг доказывает это на целом ряде примеров. Он находит золотое течение в растительном мире, в животном мире, а также в теле человека. Второе положение Цейзинга гласит, что золотое сечение господствует в архитектуре. Это доказывается, например, анализом Парфенона. В нем высота от земли до нижней линии антаблемента представляет собой большой отрезок золотого сечения, высота антаблемента и фронтона, взятых вместе, — малый отрезок золотого сечения. Цейзинг проанализировал Парфенон также более детально и построил свой анализ целиком на золотом течении. Таким образом, Цейзинг положил основание анализу Парфенона и других классических греческих зданий по золотому сечению; дальнейшие исследования разрабатывали положения Цейзинга. Третье положение Цейзинга сводится к тому, что золотое сечение в архитектуре объясняется господством золотого сечения в природе. Архитектор в своем творчестве, по мнению Цейзинга, продолжает творчество природы.

 

Жолтовский, разработав основные положения Цейзинга, дополнил их самостоятельными выводами. Так, например статую Аполлона Бельведерского Жолтовский, как и Цейзинг, делит по золотому сечению, которое Проходит по линии пупка; затем два полученных таким образом отрезка Жолтовский членит согласно отношению, которое он называет «функцией», т. е. на два отрезка, относящиеся друг к другу, как 528 и 472. Это то новое, что внес Жолтовский (рис. 1).

 

 

Рис. 1. Пропорции Венеры Милосской. По Жолтовскому

 

 

Чтобы получить малый отрезок функции Жолтовского (472), следует взять в убывающем ряде золотого сечения значение третьего порядка, которое от единицы будет 0,236, и удвоить его. Уменьшающийся ряд золотого сечения состоит из следующих приближенных значений: 1, 0,618, 0,382, 0,236. Если вычесть из единицы удвоенное 0,236, то мы получим 0,528 — большой отрезок функции.

 

Могут быть два графических способа получения функции. Можно, как чаще всего поступает сам Жолтовский, удвоить малый отрезок золотого сечения и от этого удвоенного отрезка взять вновь большой отрезок золотого сечения. При этом вы сперва удваиваете, потом члените по золотому сечению. Но можно сделать и наоборот: сначала найти золотое сечение от малого отрезка золотого сечения, а затем его удвоить. В обоих случаях результат будет один и тот же, только достигнут он будет двумя различными методами. Жолтовский берет отношение функции потому, что оно приближается к квадрату, но вместе с тем отличается от квадрата тем, что построено на иррациональных числах и в конечном счете сводится к золотому сечению.

 

Типичный прием Жолтовского состоит в комбинировании двух основных отношений: отношения золотого сечения и отношения, которое Жолтовский называет функцией.

 

При исследовании пропорций Парфенона Жолтовский идет от общего к частному: от пропорций ансамбля Акрополя к пропорциям Парфенона. Длина всего Акрополя, взятого с запада на восток (рис. 2), расчленяется Парфеноном на малый отрезок золотого сечения в середине и большие отрезки по его сторонам. При этом крайние точки Акрополя выбраны не произвольно: они определяются архитектурными частями, которые относятся к классической эпохе. Можно было бы возразить Жолтовскому, что эта закономерность зрительно не воспринимается непосредственно. Однако зрительный момент хотя и играет в греческой архитектуре очень большую роль, но далеко не настолько автономен и развит в ней, как в архитектуре Ренессанса и барокко. Повидимому, греческие зодчие давали пропорции не только с точки зрения их зрительного восприятия, но и как реальные соотношения. Расчленение на средний малый отрезок золотого сечения и на два больших отрезка золотого сечения по его сторонам является типичным для древнегреческого зодчества и встречается, например, в пропорциях коринфских капителей. При этом получается целый ряд переплетающихся между собой соотношений; в отношении золотого сечения находятся средний отрезок и правый боковой, средний и левый боковой, левый боковой и сумма двух правых, правый боковой и сумма двух левых, так как малый отрезок и большой отрезок золотого сечения в сумме дают следующий отрезок восходящего ряда золотого сечения. Именно это соотношение трех отрезков золотого сечения характерно для пентаграммы, как это подробно показано в брошюре Тиммердинга «Золотое сечение».

 

 

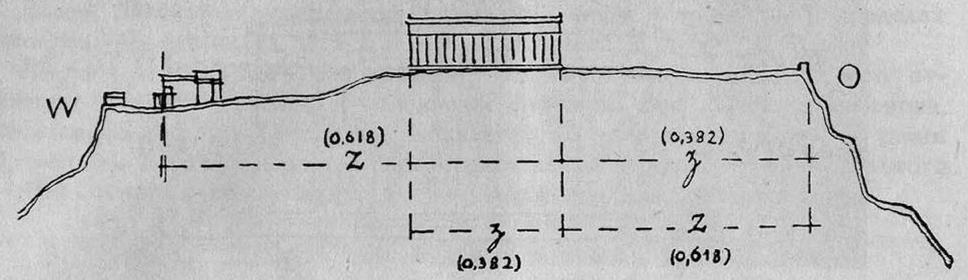
Рис. 2. Пропорции ансамбля Акрополя. По Жолтовскому

 

 

Если теперь взять ширину Акрополя с севера на юг (рис. 3) за единицу и расчленить ее по золотому сечению, то этим определяется расположение северной стороны Парфенона. Если расчленить полученный таким образом малый отрезок золотого сечения по функции, то большой отрезок функции определит собой всю ширину Парфенона, а малый отрезок функции — ширину платформы на субструкциях к югу от Парфенона. Взяв же за единицу высоту крайней южной точки этой платформы над уровнем моря и разделив ее по золотому сечению, мы получим вспомогательную точку; расчленив полученный при этом новый отрезок по функции, приняв большой отрезок этой функции за больший отрезок золотого сечения и пристроив к нему соответствующий малый отрезок золотого сечения, мы получим высоту Парфенона. При этом построении очень ясно выступает одна из основных особенностей метода Жолтовского — оперирование вспомогательными промежуточными воздушными точками, которые привлекаются в очень большом количестве. При помощи двух описанных построений Жолтовский получает наружный параллелепипед Парфенона из длины и ширины площадки Акрополя, с одной стороны, и из высоты этой площадки над уровнем моря — с другой.

 

 

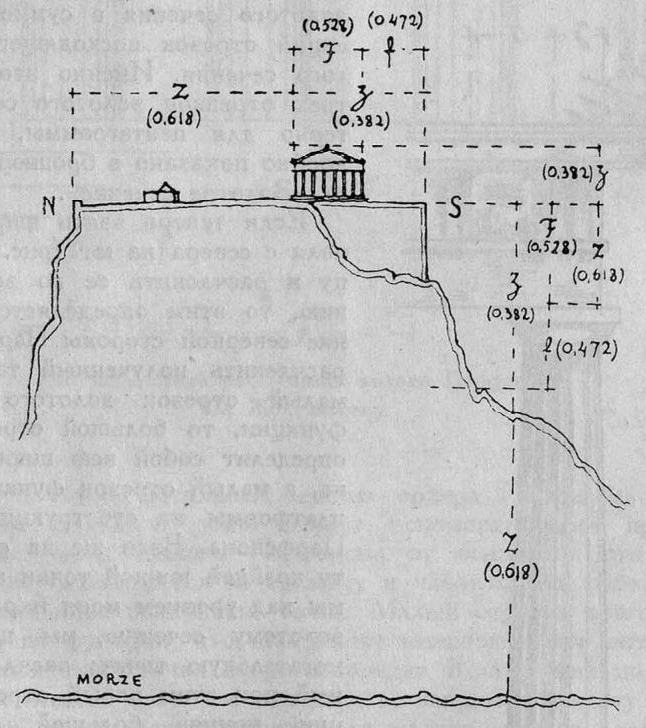
Рис. 3. Пропорции ансамбля Акрополя. По Жолтовскому

 

 

Далее, Жолтовский переходит к анализу форм Парфенона в пределах этого параллелепипеда.

 

Анализ Жолтовского основывается на комбинировании основного отношения золотого сечения и отношения функции. Вся высота Парфенона, принятая за единицу (рис. 4), разбивается по золотому сечению, и таким образом получается нижняя линия антаблемента. Малый отрезок золотого сечения членится по функции, и получается верхняя линия карниза.

 

 

Рис. 4. Пропорции Парфенона. По Жолтовскому

 

 

Затем следует более детальный анализ ордера Парфенона (рис. 5); при этом очень большую роль играют вспомогательные промежуточные воздушные точки. Высота Парфенона от основания стилобата до верхней линии карниза берется за единицу и членится по функции; получается вспомогательная воздушная точка. Малый отрезок этого членения вновь членится по функции, что определяет нижнюю часть антаблемента. При помощи воздушной точки второго порядка Жолтовский получает высоту стилобата. Можно было бы определить, например, высоту стилобата, по Жолтовскому, как большую функцию от малого отрезка золотого сечения большой функцией всей высоты здания. Аналогичным образом получается и расчленение антаблемента (ср. еще более детальные анализы на рис. 6 и 7).

 

 

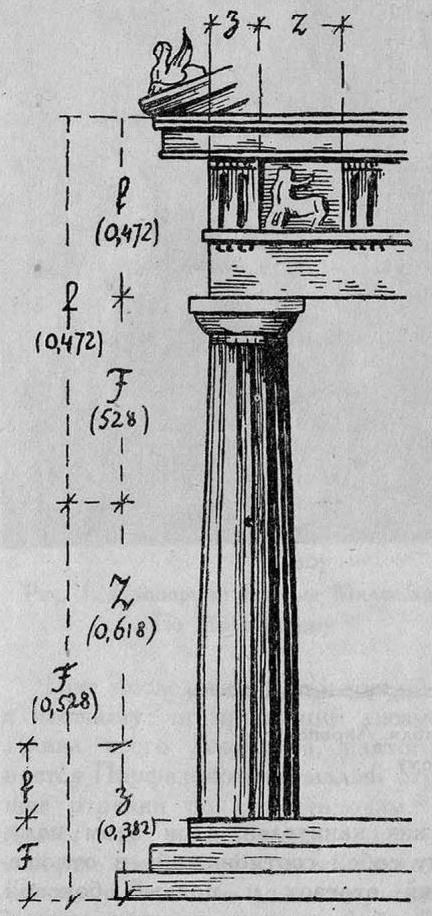
Рис. 5. Пропорции Парфенона. По Жолтовскому

 

 

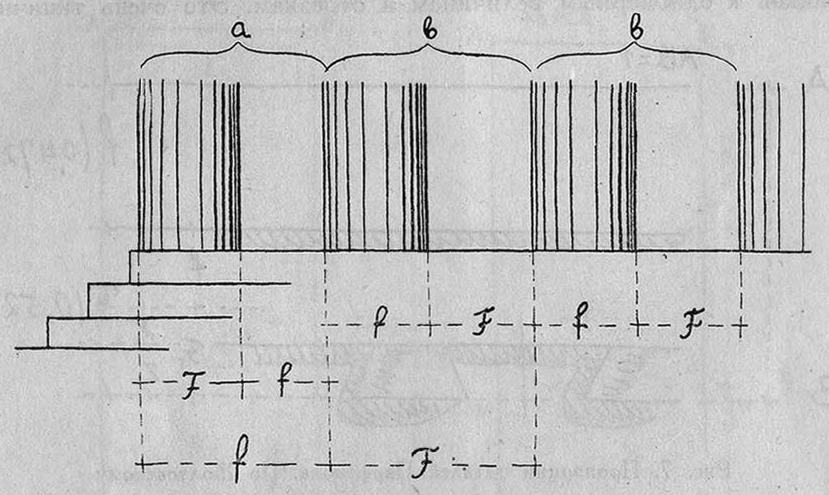
Рис. 6. Система расстановки колонн Парфенона. По Жолтовскому

 

 

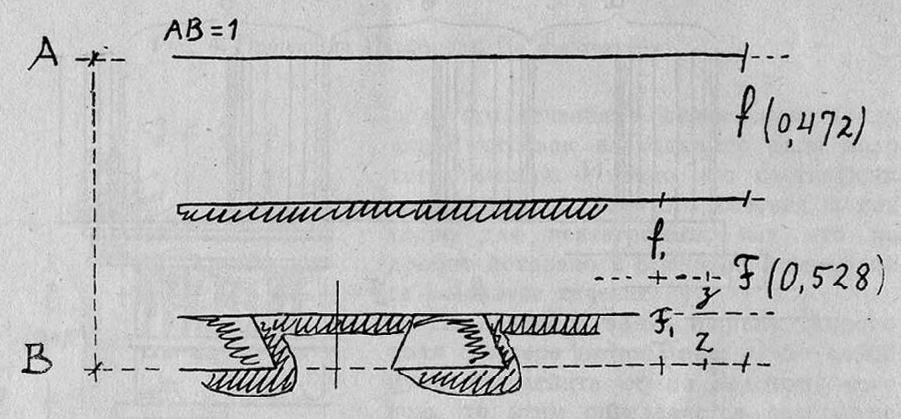
Рис. 7. Пропорции деталей Парфенона. По Жолтовскому

 

 

При анализе плана Парфенона (рис. 8) ясно выступает другая типичная особенность метода Жолтовского — оперирование исключительно отрезками, метод измерения циркулем. Прямоугольник плана разлагается на линии. Определение пропорций плана Парфенона разлагается Жолтовским на две задачи. В одной из них дана короткая сторона прямоугольника плана Парфенона, а искомым является его длинная сторона. Короткая сторона откладывается на длинной, в получившемся квадрате проводится диагональ, которая откладывается на длинную сторону, и эта диагональ рассматривается, как большой отрезок золотого сечения, к которому пристраивается малый отрезок золотого сечения. Их сумма дает длинную сторону плана Парфенона. В другой задаче дана длинная сторона и ищется короткая сторона прямоугольника плана. Вся длинная сторона членится по золотому сечению, затем большой отрезок вновь делится по золотому сечению; полученный таким образом малый отрезок удваивается, вся сумма трех отрезков вновь берется за единицу и членится по функции. Большой отрезок этого деления по функции является короткой стороной плана Парфенона. Этот метод представляет собой принципиальное сведение прямоугольников к одномерным величинам и отрезкам. Это очень типично для Жолтовского, особенно по сравнению с другими теориями, которые рассматривают прямоугольники, как неразложимые цельные данности, не сводимые к линиям.

 

 

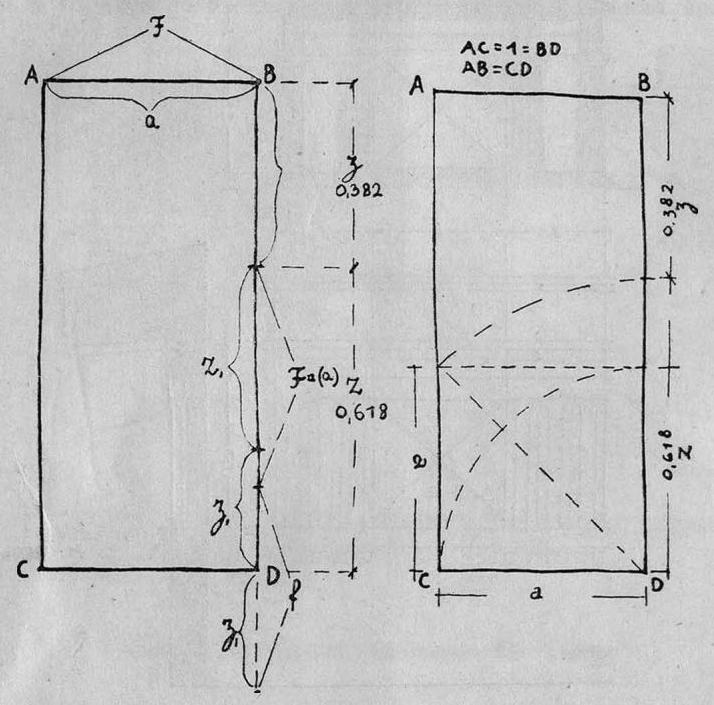
Рис. 8. Пропорции плана Парфенона. По Жолтовскому

 

 

Огромным достижением Жолтовского при изучении античных и главным образом классических греческих памятников является его блестящий и чрезвычайно остроумный анализ их пропорций. Но вместе с тем метод Жолтовского страдает, в основном, тремя недостатками. Это, во-первых, сведение всех пропорций к одномерным величинам; во-вторых, слишком свободное оперирование воздушными точками; в-третьих, несистематизированное комбинирование основных отношений золотого сечения и отношений функции. Вполне мыслимо теоретически, что древние греки комбинировали два отношения, но тогда должен был существовать закон, который лежал в основе этих комбинаций. Однако греки могли получать отношения функции другим путем. Функция является производным золотого сечения, и, подходя другим путем к пропорциям, древние греки могли получать результаты, с которыми отчасти совпали результаты анализов Жолтовского. Наконец, другие теории доказали, что в пропорциях Парфенона, кроме золотого сечения, играли роль также и иные закономерности. Поэтому исключительное сведение пропорций Парфенова к золотому сечению, как это хотел сделать Цейзинг, а также Жолтовский, является упрощением на самом деле более сложного вопроса.

 

Очень интересно указание Жолтовского на пропорциональный циркуль, найденный при раскопках Помпей и закрепленный на золотом сечении (инвентарный номер этого циркуля в Неаполитанском музее 76684). Правда, этот циркуль был найден в мастерской скульптора вместе с другими инструментами, которые, несомненно, принадлежали этому скульптору, так что он не имеет непосредственного отношения к архитектуре. Все же без особой натяжки можно утверждать, что не только древнеримские скульпторы, но и древнеримские архитекторы пользовались такими циркулями. Длина неаполитанского циркуля составляет 146 мм, отдельные ножки разбиты на отрезки в 90 и 56 мм, что дает очень точное и хорошее приближение к золотому сечению. Этот циркуль доказывает, что в Риме пользовались пропорциональным циркулем и золотым сечением.

 

Значительно сложнее оказывается дело с Грецией: были ли такие циркули в Греции или они изобретены в Риме в начале первого века нашей эры, это остается под вопросом. В дальнейшем я приведу данные, которые позволяют усомниться в том, что пропорциональные циркули были также и в древней Греции.

 

Но неаполитанский циркуль не является доказательством, что греки и даже римляне пользовались только золотым сечением, потому что имеются еще три циркуля, дошедшие до нас от античности, которые хранятся в различных музеях и поставлены не на золотое сечение, а на другие соотношения. Это, во-первых, два циркуля в Мюнхене, которые поставлены на отношение 1:2; один из них хранится в Музее прикладных искусств в Мюнхене, имеет длину 201 мм и разбит на 134 и 67 мм, другой имеет длину 219 мм и разбит на 146 и 73 мм. Третий древнеримский циркуль находится в музее Терм в Диме. Его длина — 146 мм, она совпадает с длиной неаполитанского циркуля. Длина римского циркуля разбита на 94 и 52 мм, т. е. это отношение, которое приближается к отношению 5:9.

 

Со времени Цейзинга исследование золотого сечения в природе сильно продвинулось вперед. Были, например, проанализированы с этой точки зрения раковины, и было найдено, что их спирали развертываются в некоторых случаях на основе золотого сечения. Затем указывается постоянно на растительные формы, например на цветки, в виде пентаграммы. Аналогичные исследования многократно производились над человеческой фигурой. Наконец, очень интересна работа, которая была посвящена исследованию золотого сечения в пропорциях человеческого лица. Было выбрано идеальное, с точки зрения автора, лицо, и оказалось, что это лицо вписывается в прямоугольник золотого сечения, причем главные подразделения этого) прямоугольника даны на основе отношения золотого сечения и определяют собой основные членения лица.

 

Целый ряд выдающихся специалистов оспаривают приведенные выводы и ставят под сомнение методы, при помощи которых они получены. Но приведенные попытки доказать господство золотого сечения в природе очень интересны; они безусловно показывают, что в какой-то мере золотое сечение можно найти в формах природы, но вопрос о том, в какой именно мере и каково его значение в природе, остается открытым. Привлекать для объяснения архитектуры гипотезу о золотом сечении в природе в качестве неоспоримого и доказанного положения, как это делают Жолтовский и многие другие, конечно, нельзя. Все это очень остроумные и интересные попытки, но это только гипотезы и часто очень рискованные. Анализы Цейзинга и Жолтовского античных статуй с точки зрения золотого сечения имеют очень большой смысл для изучения архитектуры. Эти анализы не доказывают, конечно, наличия золотого сечения в природе, но бесспорно доказывают, что греки мыслили себе природу построенной по золотому сечению. Анализы Цейзинга и Жолтовского очень важны и с такими оговорками; они очень многое объясняют в классической греческой архитектуре. Но только при этом вся теория золотого сечения лишается своего нормативного характера и превращается в объяснение греческой архитектуры из мировоззрения самих греков.

 

Предшественником американца Хэмбиджа, которому принадлежит другая теория о пропорциях Парфенона, является немец Тирш. Тирш первый указал, что в произведениях классической греческой архитектуры подобные прямоугольники повторяются в различных масштабах. В анализах Тирша интересно, во-первых, оперирование прямоугольниками как цельными данностями, неразложимыми на линейные отрезки, а во-вторых, мысль о созвучности отдельных частей здания. Так, Тирш сопоставляет, например, на одном чертеже разрез Парфенона и его антаблемент и показывает, что подобные прямоугольники в разных размерах определяют собой крупные части здания и его детали (рис. 9 и 10). Целое и детали определяются одним и тем же законом.

 

 

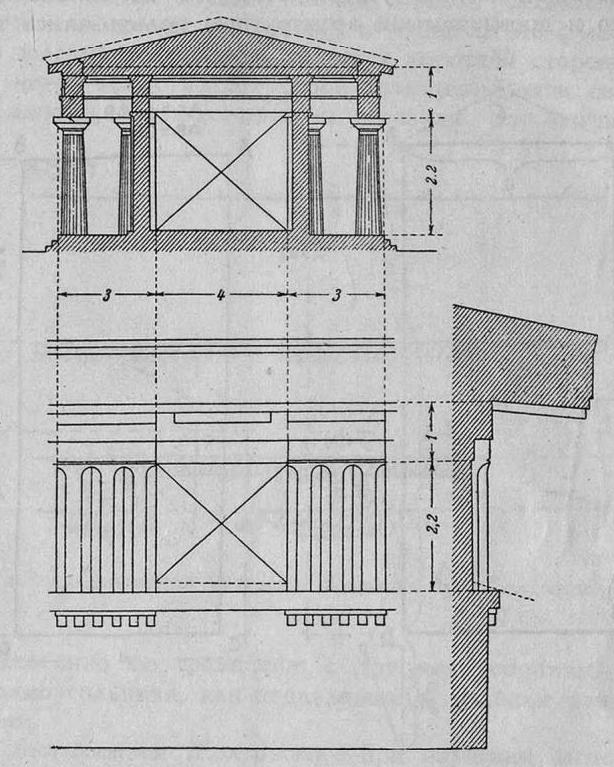
Рис. 9. Пропорции храма Посейдона в Пестуме. По Тиршу

 

 

Рис. 10. Пропорции Парфенона. По Тиршу

 

 

Основной заслугой Хэмбиджа является расширение теоретической базы учения о золотом сечении в архитектуре, базы, очень мало разработанной Жолтовским, который идет главным образом эмпирическим путем.

 

Очень существен для Хэмбиджа прямоугольник , который повторяется много раз в плане и в лицевых сторонах Парфенона. Это — прямоугольник, стороны которого относятся друг к другу, как 1 и 2,236. Исследование прямоугольника  является одной из основных заслуг Хэмбиджа. Прямоугольник  включает в себя прямоугольник золотого сечения, который вытекает из прямоугольника , имеющего более общее значение.

 

Основная мысль Хэмбиджа сводится к принципу «динамической симметрии». Под словом «симметрия» Хэмбидж понимает не симметрию в нашем смысле слова, а симметрию, как ее, по его предположению, понимали древние греки. Дословным переводом слова συμμετρία будет «соразмерность». Этим выражается принцип повторения подобных прямоугольников в различных размерах. Симметрия классических греческих зданий, по мнению Хэмбиджа, — симметрия не «статическая», а «динамическая». Хэмбидж различает статические и динамические прямоугольники. Статические прямоугольники — это те, стороны которых выражаются в простых числах; динамические — стороны которых выражаются в числах иррациональных. Принцип динамической симметрии состоит в повторении в различных размерах подобных прямоугольников, основанных на иррациональных числах. Чрезвычайно ценным является то обстоятельство, что Хэмбидж получает одновременно и пропорции плана, и пропорции узкой лицевой стороны Парфенона, и пропорции его длинной лицевой стороны. Но Хэмбидж оперирует исключительно прямоугольниками, а не трехмерными фигурами. Поэтому параллелепипед, в который вписывается Парфенон, складывается, по Хэмбиджу, из отдельных двухмерных полей, а не рассматривается им как нечто первично-трехмерное.

 

Типичными примерами статических прямоугольников являются для Хэмбиджа квадрат и прямоугольник, составленный из двух квадратов; с другой стороны, например, прямоугольник, построенный на диагонали квадрата, или прямоугольник, построенный на диагонали двух квадратов, представляют собой динамические фигуры. Прямоугольник, построенный на диагонали двух квадратов, и является, с точки зрения Хэмбиджа, главным прямоугольником Парфенона. Это и есть прямоугольник .

 

Основная система динамических прямоугольников Хэмбиджа исходит из квадрата. Проводится диагональ квадрата, которая откладывается затем на продолжении одной из сторон квадрата и служит длинной стороной прямоугольника, короткой стороной которого является сторона первоначального квадрата.

 

По теории Пифагора длинная сторона полученного прямоугольника равна , если его короткая сторона равна единице. Этот прямоугольник  — первый динамический прямоугольник Хэмбиджа. Дальше Хэмбидж проводит диагональ прямоугольника , повторяет то же самое построение и получает прямоугольник следующего порядка: по теореме Пифагора это прямоугольник  — второй динамический прямоугольник Хэмбиджа. Затем Хэмбидж повторяет ту же самую операцию, строит новый прямоугольник, и этот прямоугольник будет прямоугольником , т. е., другими словами, прямоугольником, составленным из двух квадратов. Проделав, в последний раз то же построение, Хэмбидж получает прямоугольник — свой третий динамический прямоугольник, который имеет больше всего значения в архитектурно-композиционной системе динамической симметрии. Таким образом, Хэмбидж, строит целую большую, сложную и законченную систему динамических прямоугольников, причем он доказывает, что не только прямоугольник  встречается в классической греческой архитектуре, но и другие динамические прямоугольники, т. е. прямоугольники и . Хэмбидж доказывает это при помощи анализов, памятников, а также ссылкой на литературные источники. На это указывали уже давно комментаторы Витрувия и другие авторы. Для теоретической базы Хэмбиджа основным является только что изложенная концепция, т. е. построение прямоугольника.  при помощи диагоналей последовательных прямоугольников.

 

Вторым достижением Хэмбиджа, которое непосредственно приводит к проблеме золотого сечения, является внутреннее расчленение прямоугольника . Оказывается, что, если вы расчлените одну из длинных сторон прямоугольника  пополам и, взяв половину этой длинной стороны за радиус, проведете полуокружность в сторону другой длинной стороны прямоугольника , а из точек пересечения полуокружности с противолежащей длинной стороной опустите перпендикуляры на другую длинную сторону, то в прямоугольник  окажется вписанным квадрат. Два прямоугольника, которые примыкают к этому квадрату и равны друг другу, будут прямоугольниками золотого сечения. Если короткая сторона прямоугольника  равна единице, то длинная сторона его равна 2,236 (приближенное значение ) и расчленится полуокружностью на единицу и 1,236, а последняя величина, разделенная пополам, даст 0,618. В том-то и состоит значение прямоугольника , что он включает в себя прямоугольники золотого сечения.

 

Длинная сторона прямоугольника  есть диагональ двух квадратов, или, что то же, она представляет собой гипотенузу прямоугольного треугольника, с катетами 1 и 2, т. е. она есть не что иное, как гипотенуза того треугольника, который мы всегда употребляем при геометрическом построения золотого сечения. И если вспомнить обычную формулу золотого сечения , то она представляет собой то же самое построение, переведенное на язык алгебры, потому что для получения золотого сечения от гипотенузы, которая равна , мы отнимаем единицу, а остаток делим пополам. Это геометрическое построение золотого сечения употребляется в различных вариантах. С ним связано также и построение стороны правильного десятиугольника, и стороны правильного пятиугольника, вписанных в окружность, причем легко усмотреть, что это достигается опять при помощи треугольника, гипотенуза которого равняется .

 

Прямоугольник  Хэмбиджа с его основными расчленениями обладает еще следующим свойством. Если взять прямоугольник золотого сечения и прибавить к нему квадрат, то мы получим опять прямоугольник золотого сечения, только следующего порядка. Таким образом, если взять прямоугольник, одна сторона которого равна единице, а другая 0,618, и прибавить длинную сторону к короткой, то сумма их будет 1,618, т. е. получится прямоугольник, стороны которого будут равны: одна — единице, а другая — 1,618. Это — тоже прямоугольник золотого сечения. Другими словами, можно иначе расчленять прямоугольник  на больший прямоугольник золотого сечения и на обращенный к нему под прямым углом маленький прямоугольник золотого сечения. Из этого становятся ясными алгебраические формулы золотого сечения, которые обычно приняты, т. е. .

 

Если гипотенуза прямоугольного треугольника с катетами 1 и 2 равна 2,236, то, вычтя из нее длину большого катета, получим 0,236, а это есть третье значение золотого сечения нисходящего ряда, т. е. половина малого отрезка функции Жолтовского. Отсюда вытекает следующая алгебраическая формула функции Жолтовского: 2( − 2).

 

Пользуясь этой теоретической базой, Хэмбидж обращается к памятникам классического греческого искусства. Первая его книжка была о греческих вазах. Я беру очень наглядный пример хорошего греческого кратера (рис. 11). Оказывается, если мы впишем всю эту вазу в прямоугольник, то это будет прямоугольник , причем, если этот прямоугольник расчленить прямой, которая отделяет ножку от самой вазы, то у нас в верхней части получатся два прямоугольника золотого сечения, а ножка тоже будет состоять из двух прямоугольников золотого сечения. Наконец, если описать вокруг ручек вазы прямоугольники, то получатся два прямоугольника, составленные каждый из двух прямоугольников золотого сечения. Это — типичный пример динамической симметрии.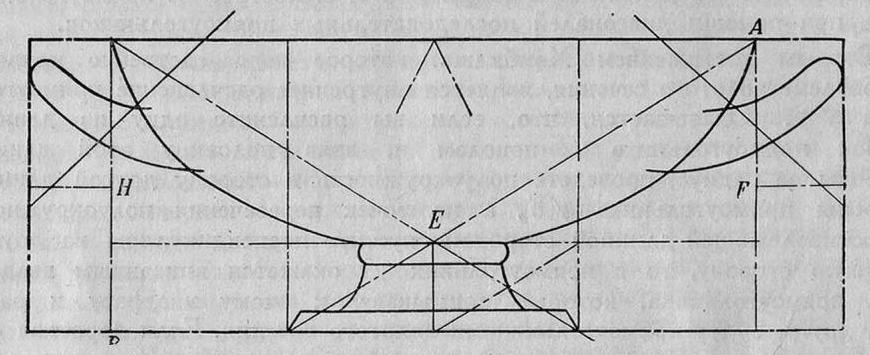

 

 

Рис. 11. Пропорции древнегреческой вазы. По Хэмбиджу

 

 

Основными прямоугольниками, которыми оперирует Хэмбидж при анализе форм Парфенона, является прямоугольник , к которому прибавляется квадрат. Если в прямоугольнике  взять за единицу длинную сторону, то его короткая будет равна 0,447. Поэтому прямоугольник, составленный из прямоугольника  и квадрата, имеет стороны, равные единице и 1,447.

 

Хэмбидж описывает узкую лицевую сторону Парфенона прямоугольником (рис. 12), затем проводит вертикальную прямую, которая членит этот прямоугольник пополам; затем, принимая половину длинной стороны общего прямоугольника за , откладывает вниз единицу и проводит горизонтальную линию, которая отделяет сверху от общего прямоугольника узкой лицевой стороны Парфенона два прямоугольника . Эта горизонтальная линия совпадает с нижней границей антаблемента. Затем каждую из длинных сторон полученных им прямоугольников  Хэмбидж делит пополам и опускает перпендикуляры на основание большого прямоугольника, причем принимает четверть длинной стороны общего прямоугольника за , откладывает вниз отрезки, равные единице, проводит новую горизонтальную линию и получает внизу четыре квадрата. Это ему нужно для анализа основных отношений Парфенона. Весь прямоугольник узкой лицевой стороны Парфенона оказывается, таким образом, разделенным на четыре квадрата и шесть прямоугольников ?5. Внизу получаются четыре прямоугольника 1,447.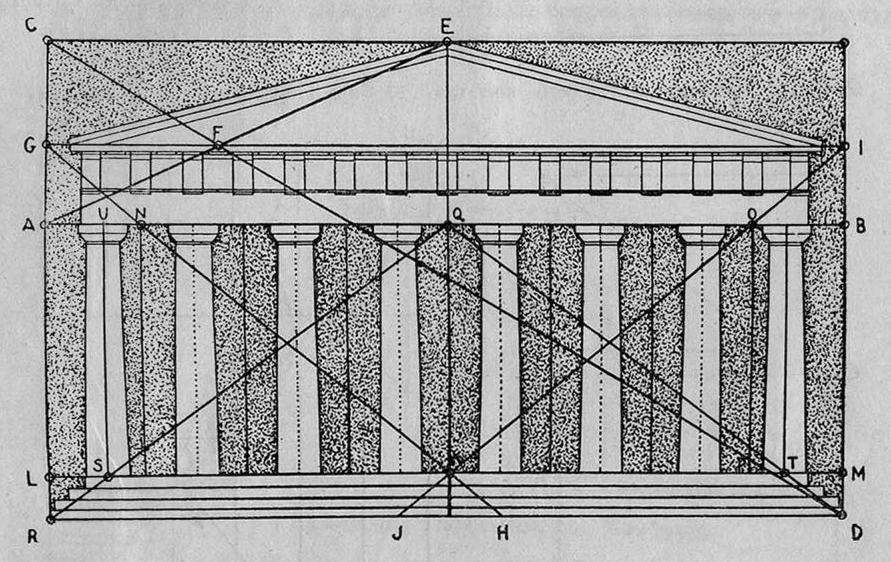

 

 

Рис. 12. Пропорции короткой лицевой стороны Парфенона. По Хэмбиджу

 

 

Расчленив указанным образом большой прямоугольник, который он описывает вокруг лицевой стороны Парфенона, Хэмбидж определяет при помощи диагоналей расположение всех основных членений Парфенона. Он проводит диагональ одного из верхних прямоугольников  и диагональ всего большого прямоугольника. Если через точку их пересечения провести дополнительную горизонтальную линию, то она совпадет с верхней линией карниза. Затем Хэмбидж через две точки основной конструкции проводят диагональ, и точка пересечения ее со средней вертикалью, делящей большой прямоугольник пополам, является точкой, через которую он проводит горизонтальную линию параллельно основной и получает верхнюю линию стилобата. Затем Хэмбидж разделяет каждый прямоугольник 1,447 пополам и получает прямоугольники, средние линии которых являются осями колонн, кроме угловых. Угловые колонны он получает, проведя диагональ через прямоугольник, состоящий из двух прямоугольников 1,447, и точка пересечения этой диагонали с линией стилобата является осью угловой колонны. Если взять прямоугольник, в который вписывается колонна, то оказывается, что он расчленяется на шесть прямоугольников золотого сечения. Это доказывает, что все построение Хэмбиджа не случайно. Боковые лицевые стороны Парфенона (рис. 13) определяются Хэмбиджем, как два прямоугольника, в которые вписываются узкие лицевые стороны Парфенона плюс отрезок длиной 0,236, т. е. половина малого отрезка функции Жолтовского, или разница между гипотенузой прямоугольного треугольника с катетами 1 и 2 и его большим катетом, равным 2.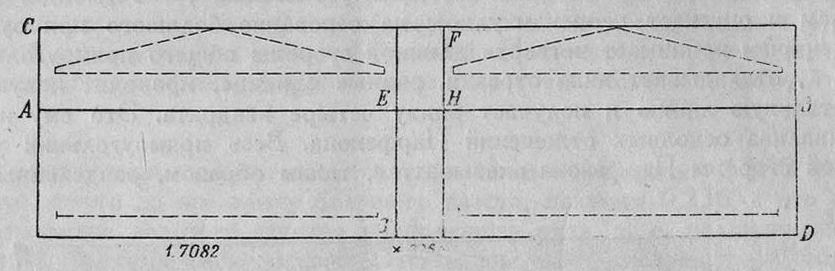

 

 

Рис. 13. Пропорции длинной лицевой стороны Парфенона. По Хэмбиджу

 

 

Чертеж, в котором Хэмбидж объединяет схему плана Парфенона и схему его узкой лицевой стороны, является самым ценным (рис. 14; ср. рис. 15). Оказывается, что план Парфенона состоит из двух прямоугольников 1,447, обращенных друг к другу под прямым углом. Между членениями лицевой стороны и членениями плана существует замечательное соответствие. Сторона каждого квадрата лицевой стороны представляет собой четвертую часть стороны большого квадрата плана. Сторона прямоугольника 1,447 лицевой стороны является четвертой частью большого прямоугольника 1,447 плана. Короткая сторона большого прямоугольника  лицевой стороны является половиной короткой стороны большого прямоугольника  плана, а короткая сторона малого прямоугольника  лицевой стороны равна половине короткой стороны большого прямоугольника  лицевой стороны. Все эти закономерности создают впечатление созвучности, соразмерности. Парфенон начинает звучать (ср. рис. 16 — образец анализа Хэмбиджа детали Парфенона).

 

 

Рис. 14. Пропорции плана и короткой лицевой стороны Парфенона, совмещенные на одном чертеже. По Хэмбиджу

 

 

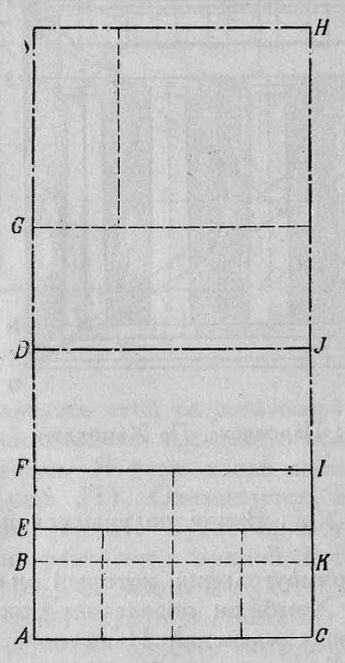
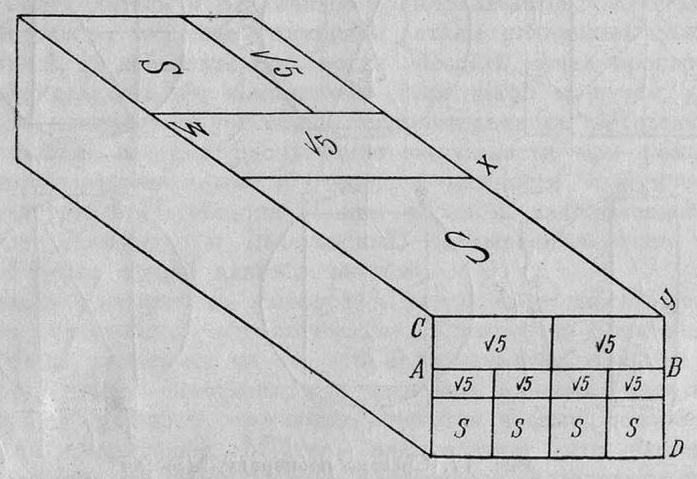
Рис. 15. Пропорции Парфенона. По Хэмбиджу

 

 

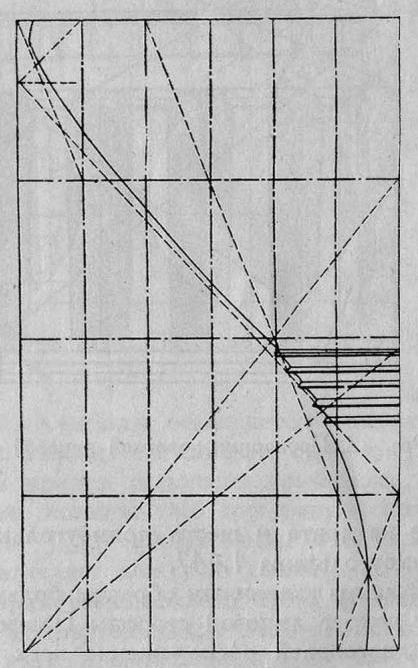
Рис. 16. Пропорции капители Парфенона.

По Хэмбиджу

 

 

Мёссель очень расширил теоретическую базу золотого сечения, даже по сравнению с тем, что дает Хэмбидж. Главная мысль Мёсселя состоит в том, что пропорции древней архитектуры основаны на расчленении окружности при помощи вписывания в нее правильных многоугольников и на построении прямоугольников на основе этих многоугольников и касательных к окружности (рис. 17).

 

 

Рис. 17. Система пропорций Мёсселя

 

 

Эта теория настолько всеобъемлюща, что отношения золотого сечения и прямоугольника  являются только частными случаями по отношению к положенной в основу ее общей закономерности. Наиболее простой метод членения окружности состоит в расчленении ее на шесть частей посредством откладывания радиуса; сюда же относится членение окружности на двенадцать частей и также более простой случай членения окружности на три части, которые являются уже производными от членения ее на шесть частей. Вторая группа — членение окружности при помощи вписывания квадрата, правильного восьмиугольника, шестнадцатиугольника и т. д. Это тоже очень простой случай, когда берется любой диаметр, под прямым углом к нему проводится второй диаметр и таким образом вписывается в окружность квадрат. Третья группа — членение окружности на пять, десять и двадцать частей. Четвертая группа встречается крайне редко. Это — очень сложное членение окружности на семь и четырнадцать частей. Методы членения окружности на шесть и четыре крайне просты. Метод членения окружности на десять частей сложен.

 

Мёссель получает, таким образом, совершенно независимо от Хэмбиджа, все три его динамических прямоугольника. Прямоугольник  получается при помощи касательных к окружности, параллельных сторонам квадрата. При делении окружности на шесть частей получается прямоугольник , что явствует из теоремы Пифагора, потому что мы имеем здесь прямоугольный треугольник, в котором малый катет равен единице, а гипотенуза равна 2. В нем большой катет равняется . Прямоугольник, построенный на правильном десятиугольнике, вписанном в окружность, и на касательных к этой окружности, состоит ив двух прямоугольников золотого сечения, потому что отношение стороны правильного вписанного десятиугольника к радиусу является отношением золотого сечения, а длинная сторона нашего прямоугольника является диаметром окружности, т. е. суммой двух радиусов. Таким образом, и отношение золотого сечения также вытекает из общих принципов Мёсселя. Но прямоугольник, состоящий из двух прямоугольников золотого сечения, является прямоугольником , к которому прибавлен квадрат, что явствует также из анализов, проделанных Хэмбиджем. Некоторое значение имеет еще прямоугольник Мёсселя, который имеет в качестве коротких сторон сторону правильного пятиугольника, вписанного в окружность. Но его противолежащие короткие стороны принадлежат двум различным вписанным в одну и ту же окружность прямоугольникам.

 

Особое место занимает у Мёсселя построение при помощи окружности прямоугольника  из прямоугольника, составленного из двух квадратов. В прямоугольнике, состоящем ив двух квадратов, сторона, общая двум квадратам, делится пополам и проводится диагональ половины двух квадратов; эта диагональ берется за радиус окружности, и таким образом при помощи касательных получается прямоугольник . Это построение основано на прямоугольном треугольнике с катетами 1 и 2, так как прямоугольник, представляющий собой половину квадрата, сам состоит из двух квадратов. Это последнее построение Мёсселя несколько отличается по методу от других его построений, поскольку оно основано не на вписывании в окружность правильного многоугольника, но все-таки и это есть частный случай деления окружности. Прямоугольник  получается методом Мёсселя при помощи деления окружности на десять частей и при помощи вписывания в окружность прямоугольника, составленного из двух квадратов.

 

Если вы приглядитесь к различным прямоугольникам Мёсселя, то они напомнят вам планы, лицевые стороны и детали различных классических греческих зданий. И действительно, когда Мёссель начал проверять свою теорию путем исследования конкретных памятников и путем указанных вычислений, то совпадения оказались поразительными. Мёссель предполагает, что именно система расчленения окружности при помощи правильных многоугольников лежит в основе, в частности, классической греческой архитектуры и Парфенона. Таким образом, закономерности, которые наблюдают Хэмбидж и Жолтовский, оказываются лишь частными случаями этой более общей закономерности.

 

Очень важно обоснование, которое Мёссель дает своей системе. Он выводит ее из предпосылок идеологических, а также из предпосылок технических. Мёссель указывает на то, что первоначально, в самые отдаленные времена, членение пространства и членение времени было подчинено одному и тому же принципу, что подтверждается часами, которые расчленяют время по окружности. Мёссель предполагает, что членение пространства и времени по окружности — магического, культового происхождения. В древневосточных деспотиях, когда архитектура была теснейшим образом связана с религией и когда она находилась под контролем жрецов, наблюдения над звездным небом дали толчок для образования системы окружности. Огромное значение имели наблюдения вроде того, например, что тень шеста описывает в течение дня полуокружность, откуда возник принцип солнечных часов. Мёссель указывает, что древнейший год был в 360 дней. Наш год в 364 дня был введен только позднее, в древнем Вавилоне. Мёссель деление окружности на 360° связывает с первоначальным годом в 360 дней. В архитектуре принцип членения окружности получил, по мнению Мёсселя, особенно широкое применение благодаря техническим предпосылкам.

 

Мёссель различает архитектуру по чертежам и архитектуру, еще не знающую чертежа. В древности, когда оперировали простейшими инструментами, пользовались для строительства главным образом простой веревкой с двумя колышками на концах, при помощи которой разбивали площадку, где предстояло возвести здание. Наши чертежи сложились только в эпоху Ренессанса. Филиппо Брунеллеско, повидимому, окончательно выработал принятую у нас систему чертежей. В древней Греции чертежа в нашем смысле слова не было, уже существовали планы, но разрезов безусловно еще не было. Кроме того, существовали наружные виды зданий, но план отличался, повидимому, эскизным характером. Чертеж зародился и развился из линий, границ частей будущего здания, которые перед строительством наносили на площадку, предназначенную для постройки. При этом-то и пользовались верейкой с двумя колышками: один колышек втыкали в землю, а другим описывали окружность. Затем окружность разбивали при помощи правильных вписанных многоугольников и получали прямоугольники, на которых основывали пропорции здания. Мёссель считает, что проблема пропорций стала эстетической проблемой только гораздо позднее. Первоначальная проблема пропорций была, с одной стороны, технической проблемой, а с другой стороны, проблемой религиозно-магической. В древней Греции наблюдается, конечно, уже сильное развитие эстетической стороны проблемы пропорций. Греческие архитекторы дали уже эстетические формулировки. Но все-таки в греческой архитектуре технические и религиозно-магические предпосылки еще играли большую роль. Это прекрасно вяжется с промежуточным положением классической архитектуры древней Греции между архитектурой Востока и архитектурой Европы. Проблема архитектурных пропорций стала самостоятельной эстетической проблемой только в архитектуре Европы, главным образом начиная с эпохи Ренессанса.

 

Перехожу к анализу пропорций Парфенона, сделанному Мёсселем. Замечательным открытием Мёсселя является проверенное на числовых данных положение, что план Парфенона по верхней ступеньке стилобата представляет собой прямоугольник  (рис. 18). Это открытие (необычайно упрощает решение плана Парфенона и вместе с тем переводит это решение от одномерных отрезков Жолтовского, от оперирования сложными прямоугольниками Хэмбиджа к очень простому и ясному положению. Ширина стилобата по верхней ступеньке берется за единицу, и Мёссель целым рядом доказательств приходит к выводу, что эта величина равнялась 100 греческим футам.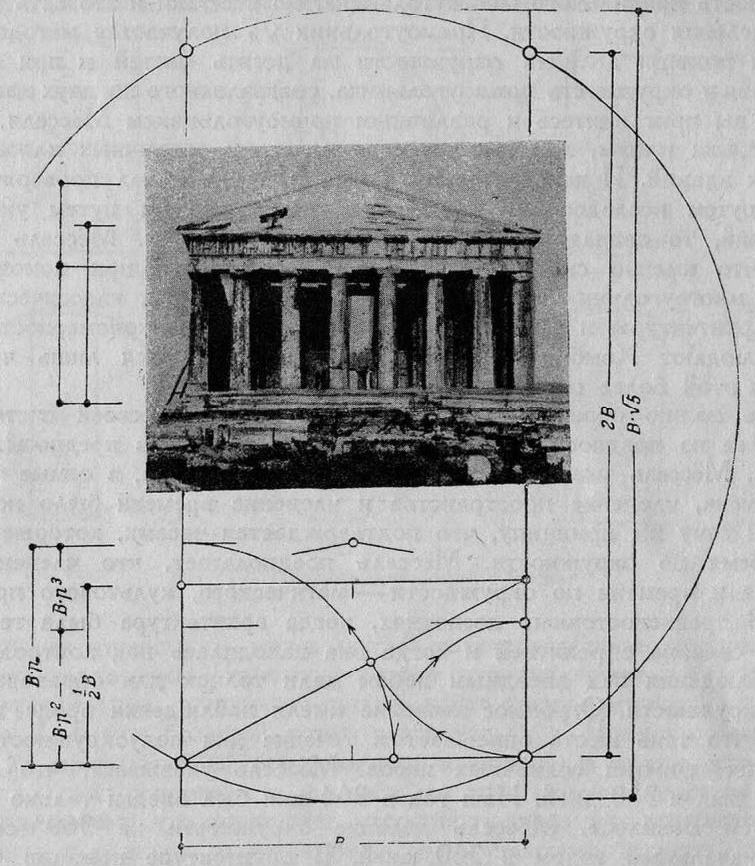

 

 

Рис. 18. Пропорции Парфенона. По Мёсселю

 

 

Второе утверждение Мёсселя сводится к положению, что расчленение плана Парфенона представляет собой нисходящий ряд золотого сечения. Внутренняя ширина целлы равна 0,618, если ширина стилобата равняется единице. Внутренняя ширина среднего нефа между колоннами внутри целлы является следующим значением уменьшающегося ряда золотого сечения. Если ширина стилобата равна единице, а внутренняя ширина целлы составляет 0,618, то ширина между колоннами целлы будет 0,382.

 

Мёссель, как и Хэмбидж, дает одновременное решение плана и лицевой стороны Парфенона (рис. 18), причем он предполагает, что начертание лицевой стороны производилось классическими греческими архитекторами также на земле, на песке. Это начертание служило для реальной отески камня здания. Имеется очень важное и любопытное подтверждение этого положения, на которое мне указал Н. А. Милютин. Оказывается, что в современном греческом судостроении употребляются аналогичные методы, т. е. до наших дней сохранилась по традиции система построения очень сложных кривых частей судов и самого корпуса при помощи веревок с колышками, посредством которых формы частей судов чертят на песке. В Керченском судостроении до сих пор сохраняется этот метод, и можно наблюдать, как старики-греки и теперь практикуют его и достигают необычайной точности формы. В классическую эпоху пользовались и в архитектуре тем же способом, как утверждает Мёссель.

 

Основной чертеж Парфенона Мёсселя (рис. 18) показывает план, который является прямоугольником . На нем строится лицевая сторона Парфенона. Откладывается вверх половина ширины стилобата, и получается прямоугольник, составленный из двух квадратов. Верхняя сторона этого прямоугольника совпадает с верхней линией карниза, так что в лицевой стороне Парфенона выделены архитекторам два квадрата. Мёссель строит диагональ этого прямоугольника, затем откладывает боковую его сторону по диагонали, а остаток откладывает на нижнюю сторону прямоугольника. Получается типичная конструкция золотого сечения. Большой отрезок совпадает со всей высотой Парфенона, меньший — с высотой Парфенона до нижней линии антаблемента. Таким образом, этот чертеж наглядно показывает, как пропорции лицевой стороны Парфенона строятся по убывающему ряду золотого сечения: если ширина стилобата равна единице, то вся высота здания равна 0,618, высота до нижней границы антаблемента 0,382, а антаблемент и фронтон, взятые вместе, — 0,236.

 

Мёсселю принадлежит еще замечательное открытие: он доказал, что пропорции колонн Парфенона получаются из расчленения окружности на двадцать частей и соединения между собой противолежащих сторон правильного двадцатиугольника, вписанного в окружность (рис. 19). Таким образом, мы получаем средний диаметр колонны Парфенона. Колонны Парфенона имеют по 20 каннелюр. Проведя две диагонали в прямоугольнике, построенном на вписанном правильном двадцатиугольнике, мы получаем каннелюры Парфенона (ср. на рис. 20 более детальный анализ Парфенона.)

 

 

Рис. 19. Пропорции колонн Парфенона. По Мёсселю

 

 

Рис. 20. Пропорции Парфенона. По Мёсселю

 

 

Очень важен еще анализ Мёсселя антаблемента угла Пропилеев на афинском Акрополе (рис. 21). Мёссель берет за центр точку пересечения угловой метопы и триглифа, а за радиус — расстояние между этой точкой и желобком ствола колонны, несколько ниже капители. Этим радиусом Мёссель проводит окружность, которую он членит на десять частей, причем сторона правильного вписанного десятиугольника оказывается равной ширине колонны по желобку. Затем Мёссель соединяет точки углов десятиугольника параллельными горизонтальными линиями, причем эти горизонтали совпадают с рядом основных линий Пропилеев. Нижняя горизонталь совпадает с желобком колонны, вторая снизу горизонталь — с нижней линией антаблемента, диаметр — с нижней линией метоп и триглифов, следующая горизонталь — с нижней линией полочки под карнизом, наконец, верхняя линия совпадает с угловой точкой карниза фронтона. Вся эта конструкция сама по себе представляет большой интерес, но особенно важно, что расстояния между горизонталями выражаются в значениях золотого сечения, которые дают очень сложную систему переплетающихся малых и больших отрезков золотого сечения. Это построение имеет большое принципиальное значение, потому что везде, где имеется расчленение окружности на десять частей, получается эта замечательная комбинация значений золотого сечения.

 

 

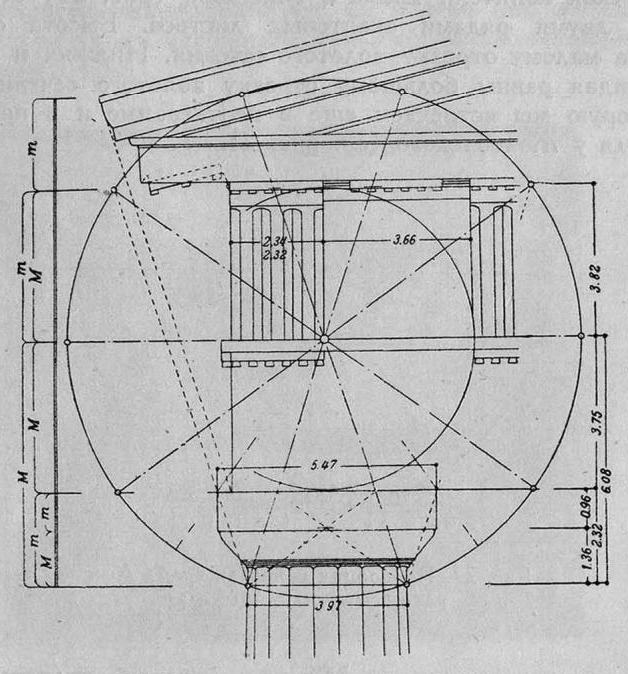
Рис. 21. Пропорции Пропилеев на Акрополе в Афинах. По Мёсселю

 

 

Отмечу еще капитель храма Афины на о. Эгине (рис. 22). Вся капитель вписывается в полуокружность. Если же вы перенесете этот плоскостной образ в трехмерное построение, то капитель впишется в полусферу.

 

 

Рис. 22. Пропорции капители храма Афины на о. Эгине. По Мёсселю

 

 

В коринфской капители храма в Эпидавре (рис. 23) основные членения даются двумя рядами акантовых листьев. Высота среднего ряда листьев равна малому отрезку золотого сечения. Нижняя и верхняя части капители каждая равны большому отрезку золотого сечения. Получается система, которую мы встречаем еще в пентаграмме и в продольном разрезе Акрополя у Жолтовского (ср. рис. 2).

 

 

Рис. 23. Пропорции капители из Эпидавра. По Мёсселю

 

 

Основной недостаток теории Мёсселя, который является недостатком и большинства других теорий, состоит в том, что он не связывает своих наблюдений над пропорциями с анализом стиля архитектурных произведений. Для Мёсселя проблема пропорций остается проблемой абстрактной: он оперирует пропорциями, как самодовлеющими понятиями, совершенно не связанными с другими проблемами архитектурного стиля. Между тем, проблема пропорций является только одной из проблем архитектурно-художественной композиции, которая теснейшим образом связана с другими проблемами архитектурного стиля и рассматривать которую изолированно нельзя. Это можно делать в качестве научного приема, но ограничиться только изучением пропорций — недопустимая односторонность. Действительно, здание, оформленное прекрасно с точки зрения пропорций, может быть совершенно неудовлетворительным, например, с точки зрения распределения в композиционном отношении его больших наружных масс или с точки зрения внутреннего устройства и т. д.

 

Абстрактность приводит Мёсселя к ошибочному основному выводу. По Мёсселю оказывается, что древний Египет, классическая Греция и средневековье имели одни и те же пропорции. На самом деле об этом не может быть и речи. Пропорции теснейшим образом связаны и зависят от общего комплекса стилистических проблем и изменяются вместе с ними. Пропорции развиваются своим собственным путем, но пропорции — это такая же историческая категория, как и всякая другая категория стиля. Не может быть и речи о том, что пропорции являются внеисторической категорией. Очень часто приходится выслушивать утверждение, что стиль здания — это только его одежда, это внешность и поверхность, а пропорция — это основное. Это — принципиально беспомощная постановка вопроса и совершенно неправильное абстрагирование и фетишизирование пропорций. Пропорции эволюционируют на основе тех же исторических изменений, общекультурных, идеологических и социально-экономических, как и весь стиль архитектуры.

 

Для Египта, Греции и готики очень легко можно это доказать на основе исследования того же Мёсселя и ряда других авторов. Так, например в Египте встречаются закономерности, приближающиеся к золотому сечению, хотя бы в разрезе пирамиды Хеопса. Половина этого разреза дает прямоугольный треугольник, в котором один катет равен 3, другой — 4, а гипотенуза равна 5. Отношение 3:5 приближается к золотому сечению, но в данном случае, это — египетский треугольник, «магический», священный. Он был «священным» не потому, что он содержит «прекрасное» отношение золотого сечения, а потому, что это — единственный прямоугольный треугольник, стороны которого выражаются в простых числах и который можно было поэтому построить при помощи палки и веревки. Именно это свойство и было причиной того, что данный треугольник объявили «священным». В Египте золотое сечение применялось совершенно иначе, чем в Греции. В Египте золотое сечение вытекало из моментов технических и религиозно-магических, причем в Египте не встречается ни уменьшающийся, ни увеличивающийся ряды золотого сечения, что особенно характерно для Парфенона и для классической греческой архитектуры. Концепция природы и человеческого тела, построенных по золотому сечению, очень подходит именно к греческому мировоззрению и, конечно, совершенно чужда мировоззрению египетскому. В отношении пропорций Египет легко противопоставить Греции.

 

Египетские архитектурные пропорции настолько же отличаются от греческих пропорций, насколько весь социальный строй Египта и его экономические предпосылки контрастируют с социальным строем и экономическими предпосылками Греции. С другой стороны, готические пропорции тоже очень сильно отличаются от пропорций греческих. До нас дошли некоторые готические чертежи архитектурных пропорций, например чертеж разреза Миланского собора, восходящий к 1391 году. Он весь построен на основе равносторонних треугольников, вписанных в окружность. Здесь теория Мёсселя всецело подтверждается. Принцип членения окружности идет от Египта, но он имеет в средние века совершенно другое художественное содержание, чем в классической греческой архитектуре или в древнеегипетском зодчестве. Этот документ доказывает, что в готике господствовала совершенно иная система пропорций: деление окружности на шесть частей, равносторонний треугольник.

 

Мы обязательно должны рассматривать архитектурные пропорции в связи с общим архитектурным стилем эпохи, но, изучая пропорции, мы должны выделить их в качестве обособленной и самостоятельной проблемы. В направлении ко все более и более обобщенной системе Мёссель еще не сделал последнего шага. Перед нами стоит проблема перехода от плоскостного решения к решениям трехмерным. Нужно не только плоскостные фигуры воспринимать, как первичную и цельную данность, но также и трехмерные формы, трехмерные блоки рассматривать, как цельные и неразложимые образы. Теорию Мёсселя нужно привести к еще более общему принципу. Трехмерная форма, из которой вытекает окружность, — это сфера, из подразделения которой мы получим все мыслимые отношения.

 

В области изучения пропорций классических греческих зданий необходимо изжить абстрактность. В связи с этим очень важно поставить вопрос о пропорциях в отношении к восприятию их зрителем, т. е. изучать пропорции с точки зрения того, как они воспринимаются глазом зрителя, стоящего на том или ином месте перед зданием. Расчет на зрителя необходимо внести; он представляет собой чрезвычайно существенный корректив к изучению пропорций в архитектуре.

 

Укажу кратко еще на некоторые проблемы, которые имеют огромное значение для вопроса об архитектурных пропорциях. Эти проблемы ставились в архитектуре очень часто и теоретически и практически, но мы их до сих пор недостаточно учитываем. Сюда относится, например, проблема объемных, линейных и плоскостных пропорций. Каждые из этих пропорций имеют совершенно самостоятельные свойства. Объемные пропорции не сводятся к плоскостным, а плоскостные не сводятся к пропорциям линейным, также и обратно.

 

Следующая проблема — пропорции архитектурных тел и пропорции архитектурных пространств, которые с точки зрения абстрактной представляют собой одно и то же. Но с точки зрения художественного впечатления на зрителя это вещи совершенно различные. Далее, например, очень важна проблема пропорций обнаженных и пропорций скрытых. В этой области открываются большие возможности для архитектора-практика, потому что одно дело — показать пропорции в обнаженном виде, выставить их на первый план, а другое дело — заставить угадывать принятые соотношения и в известный момент восприятия здания довести их до сознания зрителя. Еще другая не менее важная проблема — истолкование пропорций, как самодовлеющей области, и понимание пропорций, как средства выражения. Так, например очень часто приходится слышать, что с Микельанджело начинается «искажение» пропорций. Такая ошибка происходит именно оттого, что односторонне рассматривают пропорции различных эпох. Микельанджело пользуется пропорциями, рассчитанными на выразительность. Пропорции Микельанджело являются только языком, при помощи которого он передает в архитектуре сложные и противоречивые психические переживания. Изучение таких «субъективных» пропорций — целая самостоятельная область, которая совершенно еще не разработана, но которая имеет колоссальное значение для архитектурного образа.

 

Пропорции необходимо рассматривать, как элемент архитектурно-художественной концепции. Только таким образом можно изжить абстрактность в изучении пропорций, которая наблюдается и у практиков-архитекторов, и у теоретиков, и у искусствоведов. Пропорции представляют собой часть того единства, которое мы называем архитектурным образом. Момент выбора тех или иных пропорций является решающим, потому что пропорции в архитектуре не существуют сами по себе, вне времени и пространства, вне связи с психическим миром человека. Момент выбора тех или иных пропорций имеет свои причины. Выбор системы пропорций и разработка их зависят от идеологических и технических предпосылок, а в конечном счете — от социально-экономических предпосылок эпохи, которые всегда лежат в основе данного архитектурного стиля в целом.