Ю. Милонов. Строительная техника рабовладельческого общества. 1934

 

 

 

Автор статьи:	Юрий Константинович Милонов (1895—1980) — исследователь истории профсоюзов, истории техники. С 1931 г. заместитель директора Института техники коммунистической академии, директор Института красной профессуры техники и технической политики, затем заведующий кафедрой истории техники Московского инженерно-строительного института им. Куйбышева. Милонов в своей автобиографии отметил наиболее существенные  книги, выпущенные до его ареста в 1938 году: «Революция в технике» (1922), «История паровой машины» (1925), «Как создавались современные машины» (1928), «Развитие текстильных машин» (1929), «Сельскохозяйственные машины» (1930), «Марксистская история техники, как предмет преподавания» (1931), «Этюды по истории кинематики механизмов» (1936), «История строительной техники» в шести выпусках (1935—1937). Кроме этого, одной из тем Милонова становится история архитектуры. В середине 30-х годов он пишет работы «Технические основы архитектурных форм Древней Греции», «Архитектурные формы древнего мира», «Роль конструкции и эстетики в формировании готического стиля» и др.
Статья публикуется по изданию:	Строительная техника рабовладельческого общества / Ю. Милонов // История техники : Выпуск II / Комиссия марксистской истории техники при КВТО ЦИК СССР. — Москва ; Ленинград : ОНТИ, 1934. — 231 с., ил. — С. —88—109.
Факсимильный скан издания:	https://tehne.com/library/istoriya-tehniki-vypusk-ii-moskva-leningrad-1934

 

 

 

 

 

Второе великое общественное разделение труда — отделение ремесла от земледелия — вызвало громадные сдвиги в технике¹.

____________

¹ В разных странах это разделение произошло в различное время. В Греции оно относится к эпохе, описываемой Гомером, т. е. к X—VIII вв. до начала современного летоисчисления.

 

Уже один тот факт, что работник сосредоточил свое внимание на более узком круге предметов и средств труда, а тем самым и рабочих движений, оказал на технику очень большое влияние. «Ремесленник, совершающий один за другим различные частичные процессы, из которых складывается производство продукта, — говорил Маркс, — должен то переходить с места на место, то переменять инструменты... Орудия одного и того же рода... употребляются в различных процессах труда и, с другой стороны, в одном и том же процессе труда один и тот же инструмент служит для различных операций. Но с того момента, когда различные операции данного процесса труда обособились друг от друга... возникает необходимость в изменении орудий; служивших ранее для различных целей. Направление этого изменения формы выясняется на опыте, который показывает, какие именно особые трудности представляет пользование орудиями в их изменившейся форме²». Такова диалектика усовершенствования ремесленного инструмента. Инстинктивно, но очень отчетливо ее чувствовали многие античные писатели. «...Те, которые часто меняют свои занятия, ни одно из них не усваивают себе основательно», — писал Изократ³. «Неизбежно, что тот, кто выполняет наиболее простую работу, выполняет ее наиболее совершенно», — утверждал Ксенофонт⁴. «...Унаследовав многие правила от предков, они (ремесленники — Ю. М.) ревностно стараются, изобретать новые улучшения», — подчеркивал самую существенную сторону этого дела Диодор Сицилийский⁵. Вполне естественно, что в древности образцом промышленной страны считали Египет, где закон запрещал ремесленникам заниматься разными ремеслами.

____________

² «Капитал», т. I, изд. 8, стр. 256. (В дальнейшем все выдержки из «Капитала» цитируются по тому же изданию.)

³ Там же, стр. 278.

⁴ Там же.

⁵ Там же, стр. 255.

 

Сделавшись рынками, города, возникшие благодаря отделению ремесла от земледелия, оказали, в свою очередь, громадное влияние на дальнейшее развитие, ремесла в отношении его дробления и специализации. «В мелких городах, — пишет Ксенофонт, — один и тот же человек делает постели, двери, плуги, столы; иногда он, кроме того, строит дома и очень рад, если имеет достаточное количество подобного рода заказов, необходимых для поддержания его жизни... Но в крупных городах, где каждый работник находит много покупателей, ему достаточно знать одно ремесло, чтобы прокормиться. Зачастую даже нет необходимости знать ремесло в целом»¹.

____________

¹ «Капитал», т. I, стр. 278.

 

В новых укрепленных городах концентрируются значительные массы населения. Так, античные Афины в III в. до начала современного летоисчисления, по словам Геродота, насчитывали 30 тыс. человек²; но Афины в то время вовсе не были чем-нибудь исключительным. Тот же Геродот указывает, что они по объему примерно одинаковы с Агбатанами. Из простого убежища на время военных действий город сделался сначала центром племени, затем союза племен и, наконец, государства.

____________

² Геродот, изд. Кузнецова, 1886 г., кн. V, 97.

 

Сосредоточение значительных масс народа в городах поставило ряд проблем, не привлекавших к себе внимания в прежнее время, пока города оставались только убежищами. Наиболее важными из этих проблем были: борьба с пожарной опасностью, водоснабжение и удаление отбросов.

 

Сравнительная скученность населения в городах поставила также проблему интенсивного использования площади, охватываемой крепостной стеной, проблему, разрешенную применением многоэтажности. А многоэтажность предъявила к сооружению ряд технологических требований. «Стены кирпичные никуда не годятся, ежели не кладены в два или три ряда, — говорит Витрувий, — то есть, если их сделать только в полтора фута толщиной, не могут более одного жилья на себе снести, а сие весьма худо в таком городе, где малость места не дозволяет распространяться, однако надобно поместить бесчисленное множество жителей, то для сего необходимо подымать строение вверх»³.

____________

³ Марка Витрувия об архитектуре десять книг. Петербург 1790 г., кн. III, стр. 150 и след.

 

Но необходимость возведения солидных сооружений превратилась в возможность только в связи с другим фактором общественного развития, порожденным, вторым великим общественным разделением труда — рабством. «Непрекращающийся рост производства, — пишет Энгельс, — а вместе с ним и производительности труда повышали ценность человеческой рабочей силы. Рабство, только возникавшее и случайное на предыдущей ступени развития, теперь занимает видное место в устройстве общества; рабы перестают быть простыми помощниками: их целыми толпами гонят к работе или на поле, или в мастерскую»⁴.

____________

⁴ Энгельс, Происхождение семьи, частной собственности и государства, стр. 164.

 

Открыв возможность применения простой кооперации в больших масштабах, рабство обеспечило сооружение гигантских построек, предназначенных для того, чтобы контролировать в интересах хозяйства какую-нибудь силу природы, использовать ее или сдерживать ее разрушительные действия. «В колоссальном масштабе значение простой кооперации, — говорит Маркс, — обнаруживается в тех гигантских сооружениях, которые были воздвигнуты древними азиатскими народами, египтянами, этрусками и т. д. ... Спорадическое (в единичных случаях) применение кооперации в крупном масштабе в античном мире в средних веках и современных колониях покоится на отношениях непосредственного господства и подчинения, обыкновенно на рабстве»⁵.

____________

⁵ «Капитал», т. I, стр. 250.

 

Рабство оказало также большое влияние на характер и конструкцию орудий труда. «Рабочий, по меткому выражению древних, — пишет Маркс, — отличается здесь только как Instrumentum vocale (одаренное речью орудие) от животного, как lnstrumetum semivocale (одаренное голосом орудие) и от неодушевленного орудия: труда, как от Instrumentum mutum (немого орудия). Но сам-то рабочий дает почувствовать животному и орудию труда, что он не подобен им, что он — человек. Дурно обращаясь с ними и с истинным сладострастием подвергая их порче, он достигает сознания своего отличия от них. Поэтому считается экономическим принципом такого способа производства применять только наиболее грубые, наиболее неуклюжие орудия труда, которые как раз вследствие своей грубости и неуклюжести труднее подвергаются порче»¹.

____________

¹ «Капитал», т. I, стр. 134.

 

Это упрощение орудий шло одновременно с их продолжающейся специализацией, причудливо переплетаясь с нею.

 

Наконец, рабство явилось исходной точкой появления противоположности между физическим и умственным трудом. «...Начало искусств и наук, — говорит Энгельс, — было возможно не иначе, как при усиленном разделении труда между массами, поглощенными простой и физической работой, и немногими привилегированными, управляющими трудом, занимавшимися торговлей, государственными делами, а позже искусствами и науками. Простейшей, естественно выросшей формой такого разделения труда было именно рабство»². «Вместе с возникновением городов, крупных построек и развитием ремесла развилась и механика, — пишет Энгельс, — вскоре она становится необходимой также для судоходства и военного дела. И она нуждается в помощи математики и поэтому способствует ее развитию. Таким образом уже с самого начала возникновение и развитие наук обусловлено производством»³.

____________

² Энгельс, Анти-Дюринг, 1931, стр. 167—168.

³ Энгельс, Диалектика природы, стр. 39.

 

Усовершенствование орудий труда, разработка новых приемов работы, широкое применение простой кооперации, упрощение орудий рабского труда, наконец, возникновение науки — таковы сдвиги, произведенные в технике вторым великим общественным разделением труда — отделением ремесла от земледелия. Все это нашло отражение и в технике строительного дела, обогатившейся появлении новых орудий обработки дерева и камня, усовершенствованием каменной кладки, изобретением кирпича, разработкой системы мер пространства и инструментов измерения и развитием механики и математики.

 

 

Рис. 1. Античная пила

 

 

 

Превращение строительного дела в ремесло поставило перед обработкой дерева ряд новых требований, которым уже не соответствовал топор, оставленный в наследство предшествующим периодом. Топором можно было срубить дерево, грубо обтесать ствол, перерубить бревно, вырубить простые шипы в чашку. По топор был бессилен справиться с резкой бревна вдоль, на доски. С его помощью можно было изготовлять только тесаные доски сравнительно медленно и с очень большой потерей древесины. Между тем развитие судостроения и все более широкое применение деревянной двери, связанное с появлением частной собственности, создавали большую потребность в досках. Эта потребность могла быть удовлетворена только с началом применения в обработке дерева пиления, издавна употреблявшегося для обработки камня. Будучи воспроизведено в металле, зубчатое лезвие решило проблему доски (рис. 1). Этот этап в развитии строительной техники, нашел отражение в старинном правиле, которое общественное мнение приписало .древнему полулегендарному греческому законодателю Ликургу: «обтесывать .двери только пилой, а крышу только одним топором»⁴.

____________

⁴ Вейс, Внешний быт народов с древнейших до наших времен, изд. Солдатенкова, 1874, стр. 178.

 

Пила дала не только доску, но и брусок прямоугольного сечения. Получавшиеся при распиловке из толстых бревен прямоугольные бруски стали воспроизводиться впоследствии и при помощи топора уже из соображений декоративного порядка. Но этот способ входил в употребление очень медленно. Племена и народы, у которых ремесло еще не отделилось от земледелия, недоумевали и не принимали новшества. Есть легенда о том, что спартанец Леотикид, увидав в доме своего хозяина в Коринфе прямоугольно отесанные балки, с насмешкой спросил его: «Разве в Коринфе растут четырехугольные деревья?»¹

____________

¹ Вейс, Внешний быт народов с древнейших до наших времен, изд. Солдатенкова, 1874, стр. 180.

 

Металлическая пила быстро вошла в употребление, явившись исходной точкой значительного прогресса в обработке дерева и камня. Но ее широкое применение обнаружило один большой, недостаток, который удалось устранить только при усовершенствовании этого инструмента. Ширина пропила была равна толщине полотна пилы, вследствие чего между поверхностью пропила и боковыми поверхностями пилы возникало трение, затруднявшее работу. Терпимое при спорадическом употреблении пилы, это трение стало невыносимым тормозом при ее регулярном применении. Его устранили изобретением разводки зубьев, на которую могли натолкнуться случайно в процессе точки пилы, но сумели осознать и широко применить лишь на определенном этапе развития строительной техники.

 

 

 

Каменная кладка зародилась задолго до второго великого общественного разделения труда. Завалка еще в пещере лишних отверстий, или излишнего свободного пространства входного отверстия необделанным камнем, создавала неудобства, обусловленные большим естественным откосом каменной насыпи. При таком способе невозможно было возвести высокую стену на небольшом основании и совершенно исключалась возможность получить вертикальную поверхность. Длительная практика обнаружила, что решение задачи возможно при укладке камней друг на друга в наиболее устойчивом положении. Так возникла циклопическая кладка, т. е. кладка из больших необработанных каменных глыб, между которыми оставались значительные промежутки, заполнявшиеся мелкими камнями и глиной². Когда же в поисках удобных и плодородных пашен люди вынуждены были селиться и там, где не было пещер, каменная кладка приобрела самостоятельное значение. Воздвигали уже не дополнения к пещере, а самостоятельные стены, составляющие здания. Таким образом строили и жилые дома и крепостные стены возникавших городов. «Город, окружающий своими каменными стенами, башнями и зубцами каменные или кирпичные дома, сделался, — говорит Энгельс, — средоточием племени или союза племен: громадный прогресс в строительном искусстве, но вместе с тем и признак увеличивающейся опасности и потребности в защите»³.

____________

² Здесь сказался и опыт, накопленный в горном деле, где рано научились выводить искусственные столбы для поддержания кровли в выработанном пространстве. Вообще горное дело было отраслью, которая самым непосредственным образом связана с развитием строительного дела. Ред.

³ «Энгельс, Происхождение семьи, изд. 1932 г., стр. 164.

 

Однако малая устойчивость циклопической кладки, обусловленная случайным характером соотношений между центром тяжести и точками опоры в каждом отдельном блоке и неполным соприкосновением камней друг с другом, затрудняла возведение высоких стен, которых требовали крепостные сооружения.

 

Выход из положения был найден лишь с превращением каменной кладки в специальное занятие. Он был найден в так называемой полигональной кладке: кладке из камней, околотых с постелей и заусенков. Их клали не в один ряд, при котором швы лежали в одной горизонтальной плоскости, а соответственно многогранной форме камней, прилаживая грань к грани. Окалывание первоначально производили каменным молотком, но только из более твердой породы.

 

 

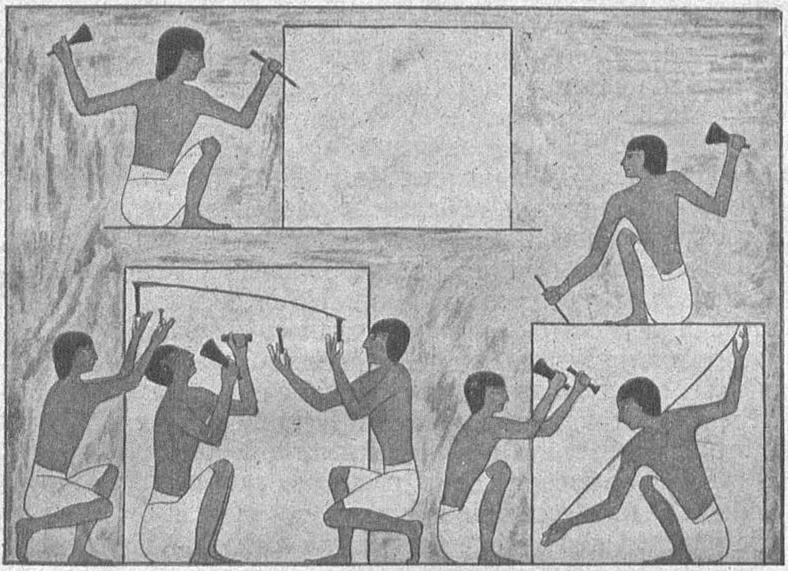
Рис. 2. Египетские каменотесы

 

 

Строительный камень откалывали от массива при помощи каменной же кирки. Но каменные орудия хорошо брали только выветрившуюся породу и были бессильны справиться с более твердыми породами. При ударе об эти последние они ломались. Скалывание кусков молота и частое переламывание его пополам на месте уха сильно тормозили работу. Только с применением металла проушина перестала быть узким местом и наиболее аварийной точкой молота, насаженного на рукоять. И лишь металлические орудия открыли возможность отесывания больших каменных блоков.

 

Применение каменной кладки вызвало ломку камня в больших количествах на местах его залегания. С этой задачей не могла справиться даже металлическая кирка. Такое затруднение заставило искать способа иным путем отламывать большие глыбы. В помощь непосредственному удару и в дополнение к нему применили клин, свойства которого были уже известны из практики раскалывания бревен¹. Сам по себе деревянный клин оказался недостаточным для отламывания больших кусков камня, но его применение натолкнуло на новый способ ломки. Просверлив в скале ряд дыр, в них вбивали клинья. При намокании (так, например, во время дождя) эти вбитые в скалу деревянные клинья сильно разбухали и образовывали в ней трещины, которые давали возможность отделять от скалы большие куски камня. Этот способ получил впоследствии очень широкое распространение.

____________

¹ А также из практики горного дела. Ред.

 

Переход в ломке камня от удара к давлению имел для техники кладки очень большие последствия. Осадочные породы, применявшиеся в качестве строительных материалов, при откалывании боковым давлением давали трещины по линиям наименьшего сопротивления по плоскости соприкосновения пластов. Таким образом получались постелистые, призматические плиты.

 

Прямоугольная форма блоков, быстро показавшая все свои преимущества, заставила тщательно отесывать строительный камень. Но с этой задачей не могли справиться ни молоток ни кирка. Здесь требовалось такое же сочетание силы удара с точностью, обеспечиваемой нажимными инструментами, — сочетание, которое давали молоток и долото. Эта комбинация была применена при отесывании камня.

 

Долото превратилось, таким образом, в шпур (рис. 2). Однако большая сподручность кирки заставила сохранить ее в качестве орудия отесывания камня при меньшем сбое.

 

Изобретение новых каменотесных инструментов, в свою очередь, стимулировало дальнейшее развитие кладки из призматических постелистых блоков. При такой кладке устранялась опасность вертикального смещения, и тем самым открывалась возможность увеличения высоты стены. Однако чем выше становилась стена, тем более ей угрожала опасность бокового смещения как в форме распадения на отдельные вертикальные столбы, так и в форме простого опрокидывания.

 

Первая опасность была устранена изобретением правильной перевязки швов. «Оные камни, лежа одни на других порядочными рядами, перевязаны, как обычно кирпичи бывают, — пишет Витрувий, — отчего стена получает свою долговечную силу»¹. Вторую задачу разрешило применение специальных подпорных насыпей. «Ничто не может столько крепости придать городским стенам и башням, как ежели сделать позади их насыпь земляную, ибо когда они таким образом подперты будут, то уже ни тараны, ни подкопы, ни прочие какие бы то ни было орудия не могут никак их раскачать», — говорит Витрувий².

____________

¹ Витрувий, кн. I, стр. 94.

² Там же, стр. 98.

 

Однако подпорная насыпь, устранявшая опасность опрокидывания стены внутрь, не гарантировала от падения ее наружу. Строго вертикальная плоскость стены, обеспечивая ее неприступность, не устраняла, однако, опасности опрокидывания. Покатая стена, наоборот, гарантировала устойчивость, но за счет неприступности. Задача сочетания противоположных качеств двух этих конструкций была разрешена изобретением контрофорсов, которые представляли собой наклонные подпорки вертикальной стены (рис. 3).

 

 

Рис. 3. Пергамский Акрополь

 

 

«Извне, — сообщает Витрувий, — надобно придать стене пристенки и упоры или быки, которые должно делать в то же время, как кладется самая стена. При этом требуется, чтобы они внизу протянулись в земле настолько, сколько высока стена, чтобы они снизу поднимались кверху, уменьшаясь постепенно, и выдавались бы кверху настолько, сколь толста стена»³.

____________

³ Там же, стр. 97.

 

Возрастающая высота стен, обеспеченная применением призматических блоков и контрофорсов, а также правильной перевязкой швов, предъявила большие и очень суровые требования к фундаменту. Если раньше в качестве основания удавалось использовать грунт путем уширения здания в форме трапеции или возведения его уступами, то теперь с увеличением массы стены этого было уже недостаточно. Тем более, что с постройкой новых укрепленных городов выбор их места определялся не наличием на поверхности подходящих для поддержки сооружения грунтов, а соображениями стратегического порядка. В поисках прочной опоры котлован стали углублять до материка.

 

«Надлежит рвы копать, — говорит Витрувий, — до самого материка, ежели можно, да и в самом материке, сколько надобно для поддержания тяжести стен, и класть фундамент из самого крепкого камня, который можно будет найти; и пускать ширину около фундамента гораздо больше, нежели как будет толщина стен сверх погребов»¹.

____________

¹ Витрувий, кн. I, стр. 97.

 

Разрешение проблемы фундамента еще больше раздвинуло границы увеличения стены сооружения.

 

 

 

Применение постелистых камней, обеспечившее возможность большего вытягивания стен вверх, в то же время создавало ряд серьезных затруднений. Прежде всего такие камни не везде можно было найти, их приходилось доставлять нередко издалека. Они требовали длительной и сложной обработки путем отесывания. Их большой вес затруднял как доставку наверх, так и самую кладку. Один камень приходилось и поднимать и укладывать нескольким работникам.

 

Пути к устранению этих затруднений строители стали искать сразу в нескольких направлениях.

 

От дальней доставки пробовали избавиться применением местного материала; от трудностей подъема и кладки — уменьшением размеров каждого блока. Однако уменьшение размеров камня было связано с удлинением процесса его обработки. Выход был найден в применении глины, пластические свойства которой были раскрыты и использованы в предшествующий период развитием гончарного дела. Из глины стали формовать на специальной деревянной доске призматические глиняные кирпичи (рис. 4). Это был как будто возврат к прошлому, к эпохе, когда глина как строительный материал широко применялась для обмазки рогожи или плетня, но возврат на совершенно новой основе — в форме воспроизведения призматического камня.

 

 

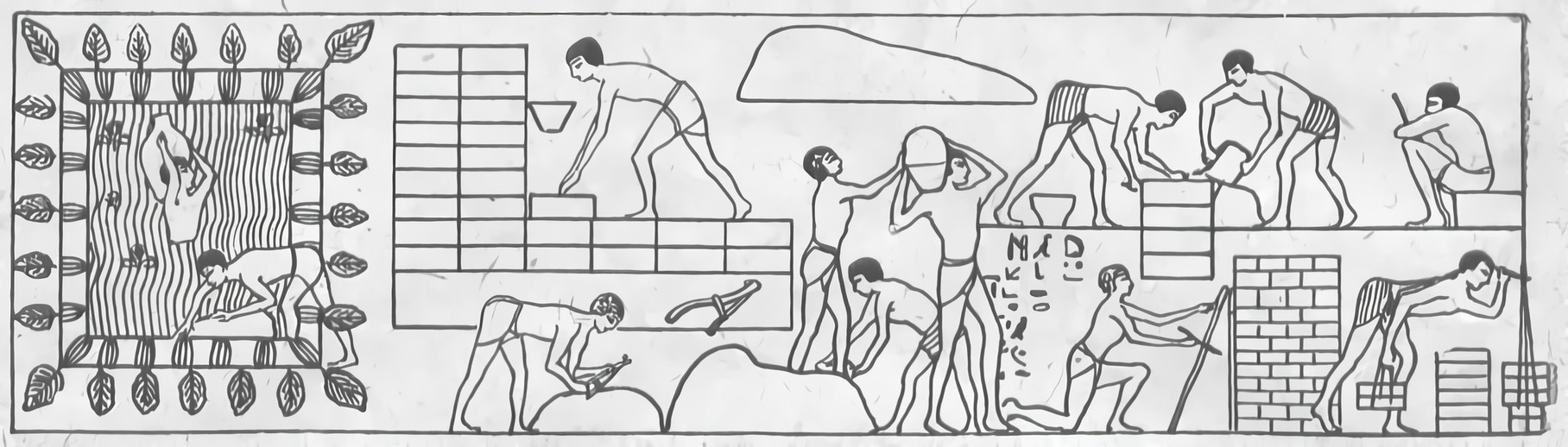
Рис. 4. Изготовление кирпича в Египте

 

 

Кирпич-сырец открыл для архитектуры громадные возможности. Так как глина широко распространена на поверхности земного шара, то благодаря кирпичу применение каменной кладки было освобождено от каких бы то ни было местных ограничений. Кирпич обеспечивал возможность более быстрого и легкого возведения высоких стен. Он-то собственно и положил начало быстрому развитию каменной архитектуры.

 

Однако кирпич-сырец имел свои существенные недостатки. Ему не хватало прочности камня. Глина трескалась и рассыпалась при ссыхании. В борьбе с растрескиванием стали применять уже разработанные гончарами приемы уплотнения глины уминанием. Стали подмешивать к глине нарезанный тростник и солому, вводя арматуру, и формовать кирпич не на дощечке, а в специальной форме.

 

Но оставался наиболее существенный недостаток кирпича — его гигроскопичность и крайне слабая сопротивляемость действию влаги. Нередко сильные ливни смывали с земли если не целые города, то уж во всяком случае целые дома. Все же преимущества кирпича были очевидны и сильнейшим образом стимулировали искание путей к устранению его недостатков. «Лучше всего, — пишет об этом Витрувий, — чтобы кирпич пролежал целые два года, ибо ежели его употребить в дело, когда он недавно отделан, и, не дав ему времени, чтобы совершенно высохнуть, наложенная на него подмазка скоро высохнет и закрепнет; а кирпич, между тем, пока станет высыхать, сожмется и осадкою своей отделится от подмазки; из сего выйдет то, что подмазка, ежели не будет плотно лежать на стене, не может сама собою держаться по причине ее тонкости, но кусками отвалится; после чего стена неравною своею во всех местах осадкою испортится и, наконец, развалится»¹. Все эти недостатки устранил обжиг, позаимствованный из гончарного дела. Обжиг дал кирпичу прочность естественного камня и тем самым на несколько тысячелетий укрепил его положение в строительной технике.

____________

¹ Витрувий, кн. II, стр. 150.

 

Прочный обожженный кирпич скоро, однако, вступил в конфликт с применявшейся до того для скрепления кладки глиняной подмазкой. Сохраняя все недостатки кирпича-сырца, эта подмазка не соответствовала новым требованиям. Благодаря ее нестойкости было невозможно добиться от стены той прочности, которую имели отдельные составляющие эту стену кирпичи. Это обстоятельство заставило упорно искать более прочной замазки. Она была найдена в виде асфальта, с одной стороны, и извести, — с другой. Асфальт был очень древним открытием человечества. Он применялся еще в каменном веке для скрепления бойков и лезвий орудий с древками. Изобретение же известкового раствора связано с периодом перехода к обожженному кирпичу.

 

Многовековая практика приготовления кирпича и известкового раствора дала ремесленникам основу и стимул для формулировки крайне примитивных, но для того времени совершенно достаточных эмпирических правил относительно строительных материалов и способов изготовления этих материалов.

 

Обжиг кирпича уже не мог производиться на костре, как это делали с посудой. 300—500°, которые мог дать костер, было уже совершенно недостаточно для обжига кирпича. Для глин, содержавших известь, требовалась температура в 950—1050°, для более бедных известью железных глин — даже 1110—1150°. Это обстоятельство заставило сильно поднять стенки очага, который, таким образом, превратился в простейшую напольную печь. В этой печи, куда вместе с кирпичом попадали куски мергеля, и обнаруживалась способность последнего рассыпаться при нагревании в белый порошок. А применение раствора такого белого порошка для побелки раскрыло вяжущие свойства отожженной гашеной извести.

 

Обожженный кирпич в соединении с известковым раствором произвел глубокую революцию в строительной технике. Такое соединение создало возможность в короткое время возводить громадные монументальные постройки, сохранившиеся в течение тысяч лет.

 

 

 

«...С возникновением городов, крупных построек и развитием ремесла развилась и механика», — говорит Энгельс².

____________

² Энгельс, Диалектика природы, стр. 39.

 

С употреблением камня строительное дело потребовало от людей передвижения и подъема очень больших тяжестей. Большие камни невозможно было ни переносить, ни поднять на постройку просто в руках или на плечах и даже на спине. Приходилось сдвигать их при помощи рычагов и тащить волоком. Принцип скольжения не годился для сухих грунтовых дорог. Выход из создавшегося положения был найден в применении салазок. Практика показала, что тяга сильно облегчалась, когда под полозья попадали палки. В этих случаях скольжение уступало место качению, при котором коэффициент трения был значительно меньше. Облегчение работы заставило сознательно подкладывать под салазки специальные обрубки дерева — катки. В конце концов стали применять несколько штук таких катков. При движении салазок они катились под полозом и, дойдя до заднего конца, выскакивали из-под него. Для удобства перевозки было необходимо, чтобы катки были под полозом все время, но это оказывалось несовместимым с самой сущностью качения. Поскольку устлать всю дорогу катками было невозможно, стали перекладывать одно и то же сравнительно небольшое количество катков, составивших теперь в руках обслуживавших повозку рабов как бы бесконечную роликовую гусеницу.

 

Этот способ передвижения был применен вслед за тем при переволакивании груженых лодок из бассейна одной реки в бассейн другой. Каток стал, таким образом, почти универсальным средством передвижения. Перетаскивание тяжестей познакомило и со свойствами наклонной плоскости. Было обнаружено, что тащить вниз по косогору легче, чем по горизонтальной поверхности, а поднимать по косогору тем легче, чем меньше его наклон.

 

Еще большие трудности, чем доставка строительного материала на место, создавало поднимание его на стену. Поднять камни на веревках по вертикали можно было только на очень незначительную высоту. И вот, когда высота вступила в конфликт с этим приемом поднимания тяжестей, в поисках способа решения задачи стали применять ту же самую наклонную плоскость, которая так часто выручала при подтаскивании материала к месту постройки. Стали возводить насыпи, по которым и втаскивали наверх каменные глыбы.

 

Для поднимания тяжестей применили также изобретенный задолго до того блок. Широкое применение блока (рис. 5) послужило базой для его научного исследования. По сообщениям античных писателей первым за изучение блока взялся Архит Таррентский (V в. до начала современного летоисчисления). Однако, что именно он внес в учение о блоках, неизвестно, так как его сочинения не сохранились.

 

 

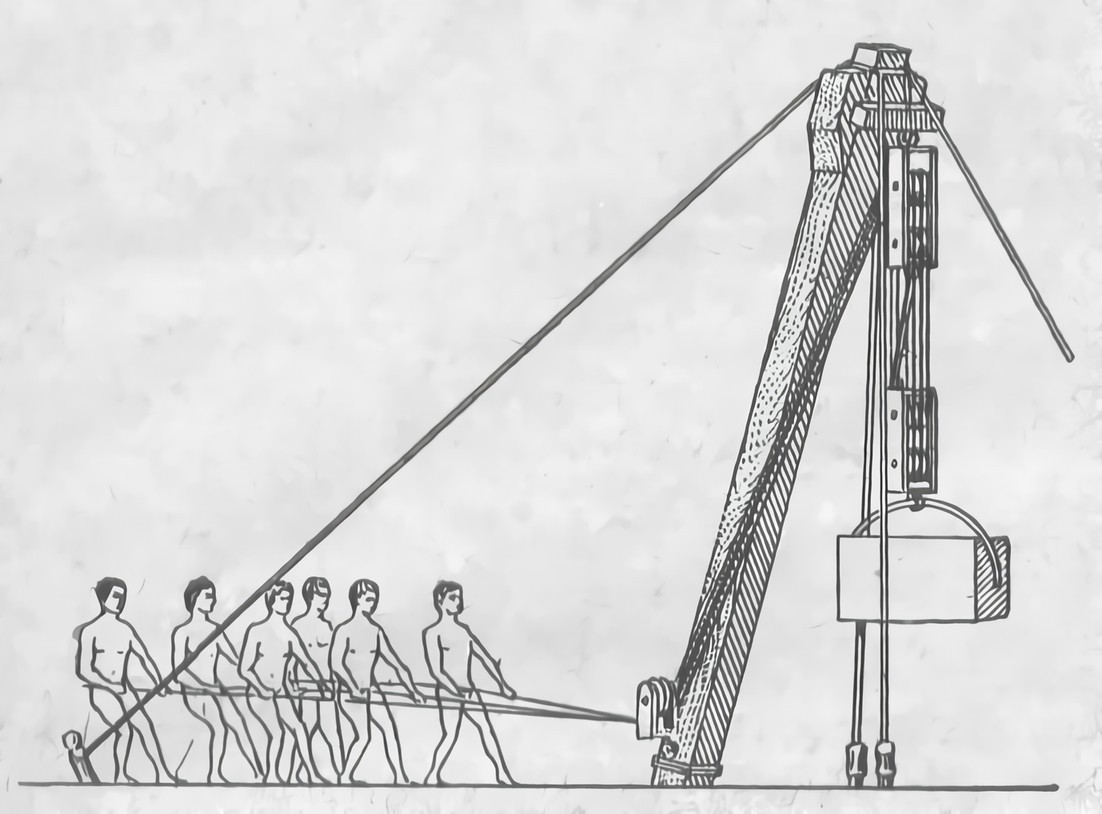
Рис. 5. Римский кран.

 

 

Повидимому, именно блок имел в виду Аристотель, когда он в своих «проблемах механики», говоря о рычаге, где «меньшее осиливает большее, маленькая тяжесть поднимает большие», писал:

 

«Основная причина всего этого заключается в существе круга и притом весьма естественно, ибо ничего нет несообразного в том, что из чудесного выходит что-нибудь чудесное. Самое же чудесное есть объединенная связь противоположных свойств.

 

Круг же есть на самом деле такая связь. Он создается даже чем-нибудь движущимся и чем-нибудь остающимся в покое»¹.

____________

¹ Цитирую по книге Э. Маха, Механика, 1909, стр. 17.

 

В результате практического пользования рычагом у руководителей строительными работами накопились сведения о его свойствах и навыки применения этих свойств. Проблема выяснения свойств и законов рычага, правда, в довольно туманной и незаконченной форме, была поставлена еще Аристотелем. Аристотель сравнил движение частей рычага и перемещение в одно и то же время на разные расстояния конечных точек радиуса или отрезка диаметра в круге.

 

Основы учения о рычаге были заложены только Архимедом. Он исходил из двух положений: величины одинаково тяжелые, действуя на равном расстоянии (от точки опоры), находятся в равновесии. «Если же они действуют на неравном расстоянии, то в равновесии не находятся, а действующая на большем расстоянии опускается». Эти положения, повидимому, опирались на практику взвешивания при помощи безмена, широко распространенного в те времена среди торговых народов, живших по берегам Средиземного моря.

 

Из формулированных выше положений Архимед сделал вывод, что соизмеримые величины находятся в равновесии, когда расстояния их (от точки опоры) обратно пропорциональны их массам. Таким образом Архимед выяснил отношение между грузами и плечами, которое было нужно знать для лучшего использования рычага. Он дал объяснение законов действия рычага, обобщив действие коромысла безмена.

 

Ход его мыслей был таков. Два груза, равные между собой, подвешены к концам стержня, который может вращаться около середины. Они находятся в равновесии. Если стержень с грузами подвесить на перекинутой через блок веревке за середину, то на конец этой веревки придется повесить груз двойного веса (если считать стержень невесомым). Это означает, что равные грузы на концах заменяют двойной груз в середине. На концы коромысла, одно плечо которого вдвое больше другого, вешаются грузы весом один вдвое меньше другого. Больший груз можно заменить двумя меньшими, подвесив оба их на равном расстоянии от точки привеса. Равновесие не изменяется.

 

К плечам рычага, относящимся как 3:4, Архимед подвешивал грузы, относящиеся как 4:3. Затем он удлинял меньшее плечо на 4, большее на 3. А грузы 4 и 3 заменял четырьмя и тремя парами симметрично подвешенных грузов 1:2. И он получал в результате полную симметрию, т. е. равновесие. Это обозначало, что любой большой груз можно заменить несколькими малыми, которые прикреплены через равные промежутки к стержню, привешенному за середину, в точке подвеса большего груза к коромыслу. Обобщая эти данные, Архимед установил отношение обратной пропорциональности между грузом и плечом.

 

Особенно остро проблема равновесия встала при возведении перекрытия.

 

Очень часто в результате нарушения законов равновесия еще до замыкания, обе ветви возводимой напускной с двух сторон арки не выдерживали и обваливались и, уже развалившись, упирались друг в друга. Нижние кирпичи оставались в прежнем положении, а верхние оказывались заклиненными. Это дало стимул и основание к применению арки, построенной на принципе заклинивания (клинчатая арка).

 

Поскольку арка была невелика, ее выкладывание не требовало особых приспособлений. Но клинчатая арка разрешала одно крайне важное и неудобное противоречие стрельчатой арки, выкладываемой напуском; противоречие между шириной и высотой. Чем шире был пролет арки, тем выше приходилось поднимать стрелу. Поэтому напускная арка была вообще неудобна для широких пролетов, появившихся в результате развития больших и сложных сооружений.

 

Обычную стену можно было ровно вывести при помощи отвеса и уровня, не задумываясь особенно над законами равновесия. В совершенно ином положении оказывались строители, когда они кроме стен начали выкладывать арки, в особенности в их первоначальной форме в виде арки напуском. Здесь камни держались только в том случае, если центр тяжести лежал над плоскостью камня, служившего основанием. А вся постройка не падала лишь при том условии, если напуск был мал и проекция центра тяжести находилась внутри площади опоры. Но положение менялось, когда замыкали арку. Тогда обе стороны равнобедренной арки подпирали друг друга и не падали. Однако во время самой кладки все затруднения оставались.

 

Исследованием законов равновесия для поверхностей самой разнообразной формы занимался Архимед. В своей книге о центре тяжести он дает математические способы решения этой задачи. Из рассуждений его видно, что он в своей работе исходил из техники кирпичной кладки. Определяя центр тяжести треугольника, Архимед представляет его себе разрезанным на узкие полосы, параллельные одной из его сторон. И каждую из этих полос он изучает на основе им же открытого закона равновесия рычага. Найдя, таким образом, что центр тяжести на медиане, он пришел к выводу, что это есть точка, лежащая в пересечении двух медиан. Взяв за исходную позицию анализ треугольника, Архимед исследовал четырехугольник, разбивая его на треугольники, а затем многоугольники, представляя их состоящими из четырехугольника и треугольников.

 

 

 

«...Самый плохой архитектор, — говорит Маркс, — от наилучшей пчелы с самого начала отличается тем, что, прежде чем строить ячейку из воска, он уже построил ее в своей голове»¹.

____________

¹ Маркс, Капитал, т. I, стр. 120.

 

Необходимым условием сооружения сколько-нибудь сложной постройки вроде места общественных собраний или крепостной стены является предварительный математический расчет, изготовление хотя бы примитивного чертежа и постоянные измерения в ходе самой стройки. Ремесленникам — каменотесам и строителям — приходилось на каждом шагу измерять длину, ширину и толщину каменных плит, высоту стен и колонн, ширину дверей, окон и т. п.

 

В качестве меры они воспользовались своим естественным орудием труда — рукой. Рабочие движения каменотеса или кладчика сводились к толчкам и ударам, в которых большую роль играла локтевая часть руки. Ею стали пользоваться в качестве измерительной единицы. Однако она не годилась для измерения величин меньших, чем локоть; диаметра бревен, длины и ширины врубок и пазов. Используя в качестве орудия измерения ту же руку, стали применять ширину ладони — «пальму» — и для еще меньших величин ширину пальца. В некоторых случаях употребляли промежуток между концами расставленных большого и указательного пальцев, так называемую пядь. А в качестве более мелкой единицы пользовались шириной большого пальца на уровне основания ногтя.

 

С течением времени все эти меры стали приравнивать к величине локтя, рассматривая их как части локтя. Так, локоть делили на шесть ладоней, каждую же ладонь, в свою очередь, подразделяли на четыре пальца. Эти соотношения соответствовали действительным пропорциям нормальной мужской руки, и, таким образом, каждый работник являлся обладателем сразу трех измерительных единиц.

 

Но такие меры оказались неудобными для измерения больших величин: высоты и длины стен. Тогда, продолжая традицию, воспользовались величиной своего роста, вместе с рукой, поднятой кверху, и расстоянием между концами рук, раздвинутых в стороны. Первая мера получила название косой, а вторая маховой сажени. Косая сажень считалась равной расстоянию наискось от пятки левой ноги до конца вытянутых пальцев правой руки. Воспользоваться ростом человека в качестве единицы было вполне естественно при измерении уровня потолка и высоты двери потому, что сама измеряемая величина должна была соответствовать как раз именно человеческому росту. Сажень маховая равнялась размаху руки: расстоянию между концами вытянутых пальцев. Первоначально она служила единицей для измерения ширины дверей в сараях и ворот во всевозможных изгородях.

 

Наиболее удобным орудием измерения плана сооружений была ступня (воспоминание об ее применении сохранилось до настоящего времени в виде фута).

 

Но непосредственно локтями и ступнями ног измерять очень большие величины, например стены строений, было не только неудобно, но и невозможно. Тогда воспользовались веревкой. На египетских рисунках, оставшихся от той поры, изображены ремесленники, отмеривающие маховую сажень при помощи куска веревки (рис. 2).

 

Футовые линейки изготовлялись с большой тщательностью, бережно сохранялись и передавались часто от отца к сыну. Вначале их изготовляли те, кому ими приходилось пользоваться, а в дальнейшем, с развитием ремесла, этим делом стали заниматься специальные мастера.

 

На базе применения в строительном деле этих мер сложилась мысль о воспроизведении в зданиях пропорций человеческого тела. «Итак, — пишет Витрувий, — когда природа таким путем устроила тело человеческое, что каждый оного член имеет с целым некоторую соразмерность, то не без причины древние хотели, чтобы во всех их произведениях таковое отношение частей к целому во всей точности наблюдаемо было...; разделение размеров во всех зданиях взято также с частей тела человеческого, как, например, дюйм, пальма, фут, локоть, и разделения были произведены к совершенному числу, «телион» греками называемому».

 

В тесной связи с развитием измерений стоит изобретение отвеса и угольника.

 

Мы указывали уже, что проблема устойчивости была разрешена применением призматических постелистых блоков. Однако при этом встал вопрос о соотношении центра тяжести и площади опоры уже в целом сооружении. При кладке высоких каменных, а тем более кирпичных стен строители на практике убеждались в необходимости возводить стену совершенно отвесно. Иначе она со временем давала трещины и даже совершенно разваливалась.

 

Какое громадное значение имела проблема устойчивости при сооружении высоких стен, показывает, например, легенда о Вавилонской башне (рис. 6), т. е. вавилонских пирамидах, носивших название «циккурат». Если поискать «земное ядро причудливых религиозных представлений»¹, нашедших отражение в этой легенде, то в ней легко обнаруживаются следы удивления кочевников перед городскими постройками оседлых земледельцев, использования в строительном деле иноземных мастеров (смешение языков) и неумения решить проблему устойчивости. Это последнее обстоятельство заставило пользоваться рядом приспособлений, дававших возможность точно определять вертикальную и горизонтальную плоскость. Такими приспособлениями явились отвес и угольник.

____________

¹ «Капитал», т. 1, стр. 281.

 

 

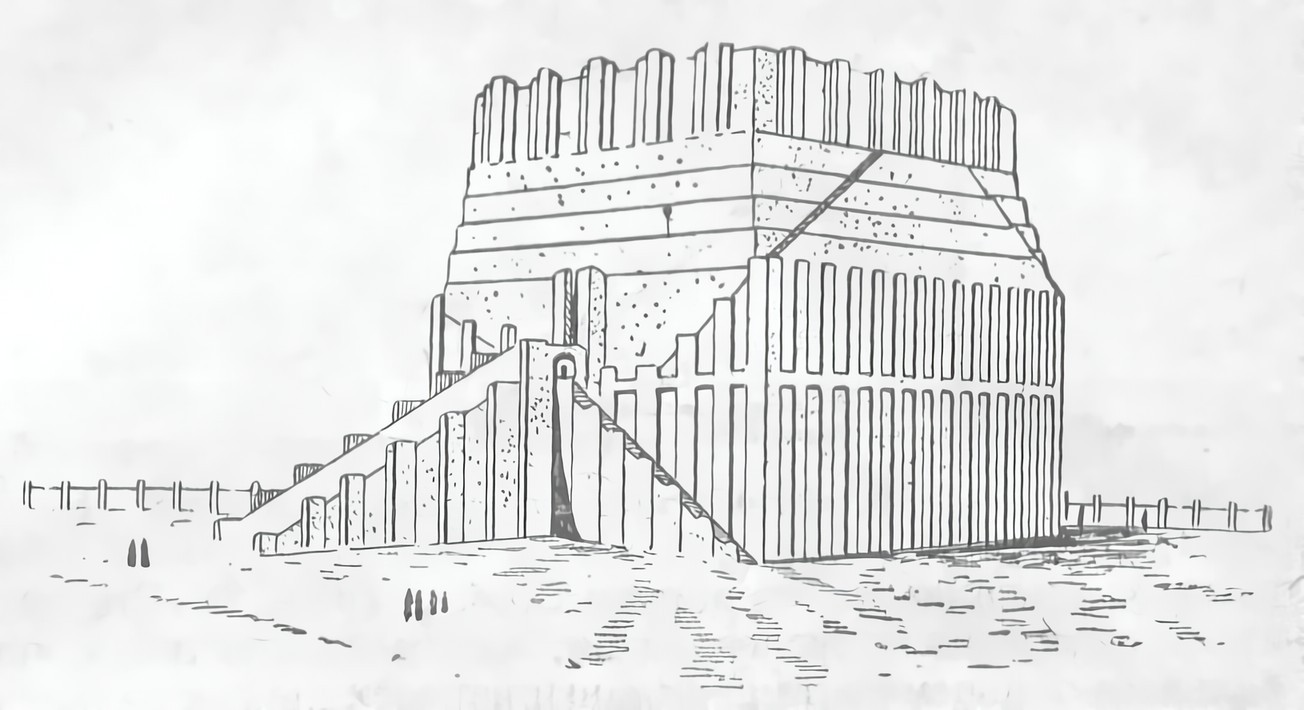
Рис. 6. Реконструкция вавилонской пирамиды (циккурат)

 

 

В изобретении обоих этих приспособлений большую роль сыграла веревка, которой пользовались и как средством поднимания тяжестей, и как орудием измерения пространства. Подъем на стену при помощи веревки строительных материалов (рис. 7) создал и понятие отвесной линии и самый прибор для ее определения, бывший простым воспроизведением грузоподъемной веревки. Применение отвеса, который давал прямой угол к горизонту, натолкнуло и на идею угольника. Стремление воспользоваться для построения прямого угла той же самой веревкой, которой измеряли длину, ширину и высоту строительных камней, оконные и дверные проемы и определяли отвесное расположение стен, натолкнуло на открытие так называемого «египетского треугольника» со сторонами 3, 4, 5 (рис. 8). Его дала двадцатеричная система счисления, обусловленная, как и десятеричная, пальцевым счетом, когда большим пальцем считали фаланги четырех других пальцев на той же руке.

 

 

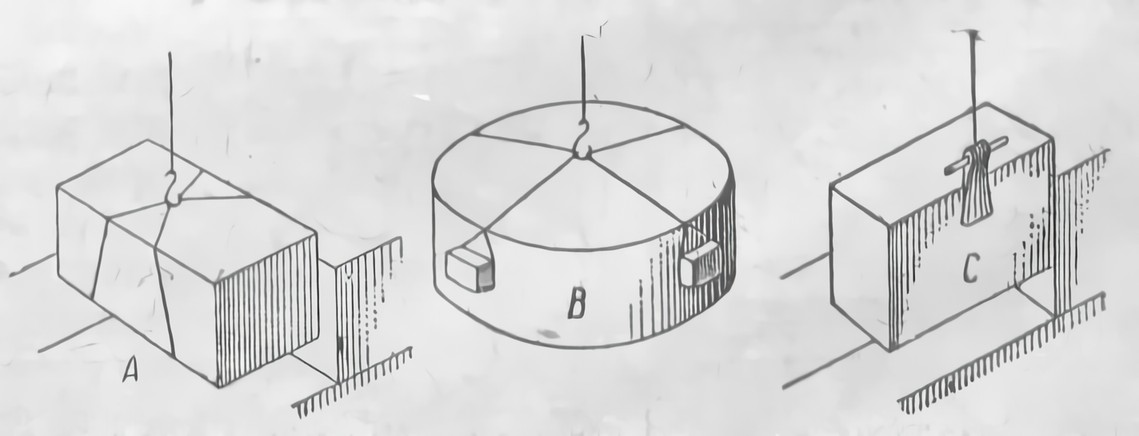
Рис. 7. Римские приспособления для поднимания материалов

 

 

Практика построения треугольника с помощью разделенной на двадцать частей веревки обнаружила, что из таких треугольников прямоугольным является только один — со сторонами 3, 4, 5. Когда же была найдена математическая формула прямого угла, его стали воспроизводить в дереве в виде всегда готового к употреблению измерительного инструмента, чего не могла обеспечить веревка, которую требовалось растягивать при каждом измерении.

 

 

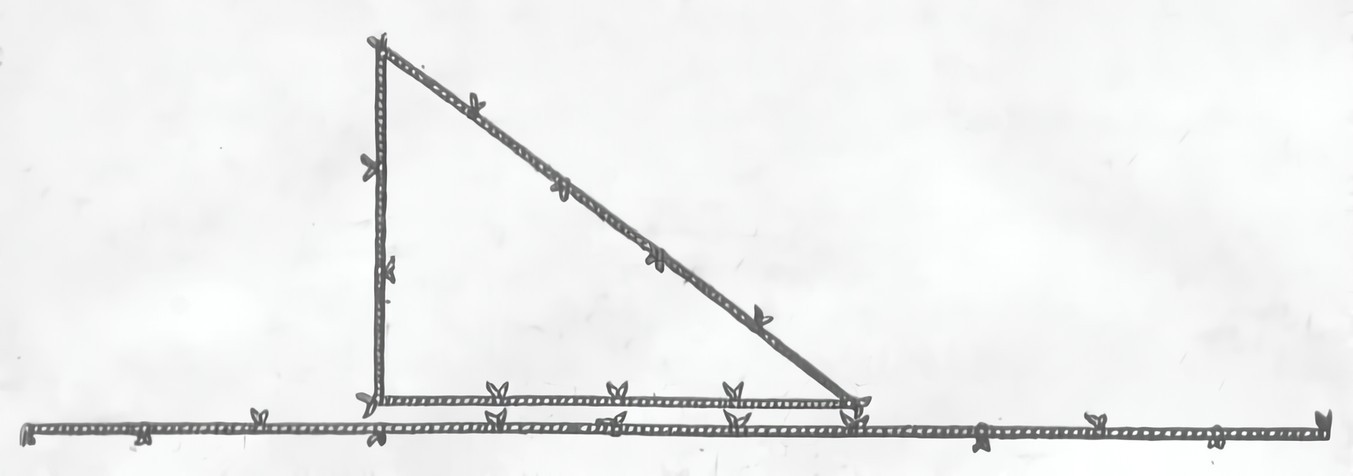
Рис. 8. «Египетский» треугольник

 

 

Как оценивало античное общество роль изобретения отвеса и угольника, видно из мифов о сказочной механике и строителе Дедале. В образе Дедала воплощены успехи строительной техники эпохи перехода от варварства к цивилизации. Ему приписывается изобретение чуть ли не всех инструментов строителя (рис. 9) и в первую голову угольника с отвесом.

 

 

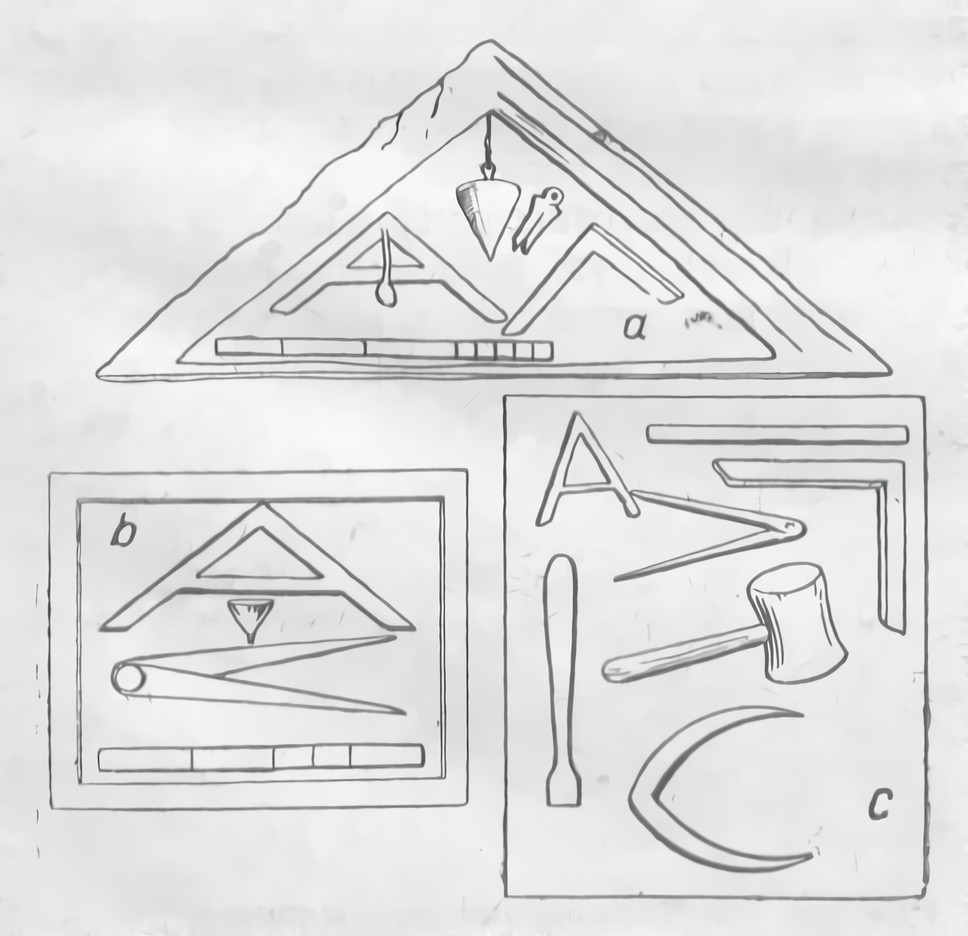
Рис. 9. Орудия римского каменщика

 

 

О роли отвеса и угольника очень красноречиво говорит римский поэт философ Лукреций:

 

«Так, при постройке домов: если первые линии кривы, если угольник не прям и от правильных черт отступает, и уклоняется уровень в неких частях хоть немного, то неизбежно окажется здание все криво и косо. Криво, нескладно, изогнуто будет нестройное здание, будто готовясь упасть, и действительно падает часто. Лишь от того, что неправильны первые были начала»¹.

____________

¹ Лукреций, О природе вещей, изд. Собашниковых, 1913.

 

 

 

Энгельс подчеркивает, что механика этого периода «нуждается в помощи математики и поэтому способствует ее развитию»².

____________

² Энгельс, Диалектика природы, стр. 39.

 

Строительная техника дала дальнейший толчок уже сильно развитой математике.

 

Изобретение призматической каменной кладки с правильной перевязкой швов и архитравного перекрытия привело к тому, что в конструкции применялись только вертикальные силы, никогда не переходящие в боковой распор. Это придавало античным каменным сооружениям громадную прочность, позволившую им простоять тысячи лет.

 

Смещение камней в кладке могло явиться результатом или недостаточной прочности материка, или следствием землетрясений, чрезвычайно частых и в Египте, и в Греции, и в Риме. Средство борьбы с этой опасностью было найдено в виде связей отдельных блоков скобами и пиронами (рис. 10). Египетские строители применяли деревянные скобы в форме ласточкиного хвоста, микенские архитектора заменили непрочное дерево более прочной бронзой, наконец, греческие зодчие заменили бронзу железом. Для укрепления скоб в камне применяли заливку свинцом. Однако эти меры были паллиативом, так как опасность коренилась во внутренней конструкции здания, именно в композиции его колоннады. Являясь значительным массивом, антаблемент и фронтон сильно поднимали центр тяжести портика, вследствие чего здание утрачивало свою устойчивость и при землетрясении колоннады опрокидывались наружу. Еще хуже дело обстояло с постройками из сырцового или примитивного плохо обожженного кирпича. Возводимые из такого кирпича постройки, не подвергаясь боковому распору, нередко разваливались под влиянием собственного веса, в особенности в тех случаях, когда постройкам старались придать гигантские размеры и призматическую форму (рис. 6).

 

 

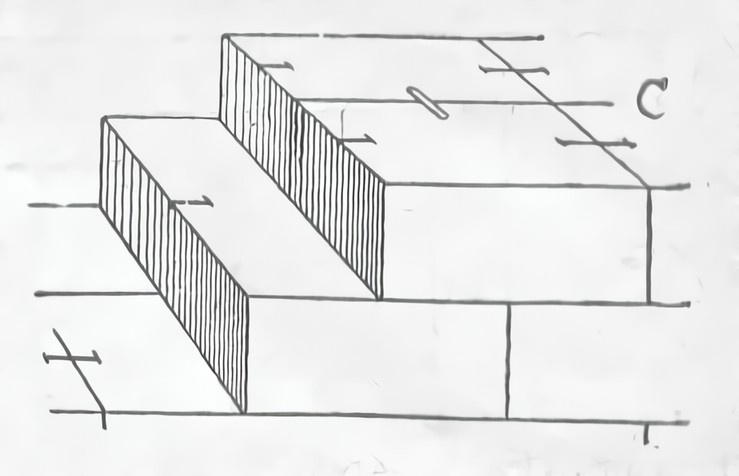
Рис. 10. Связывание блоков скобами

 

 

Легенда о Вавилонской башне отражает катастрофы этого рода. В поисках способов преодоления разрушительного действия собственного веса строители, эмпирически, может быть, воспроизводя форму оставшихся руин, пришли к профилю равного сопротивления. К нему приближаются египетские пирамиды (рис. 11), имеющие вполне определенный угол наклона стен — в большинстве 40 или 50°.

 

 

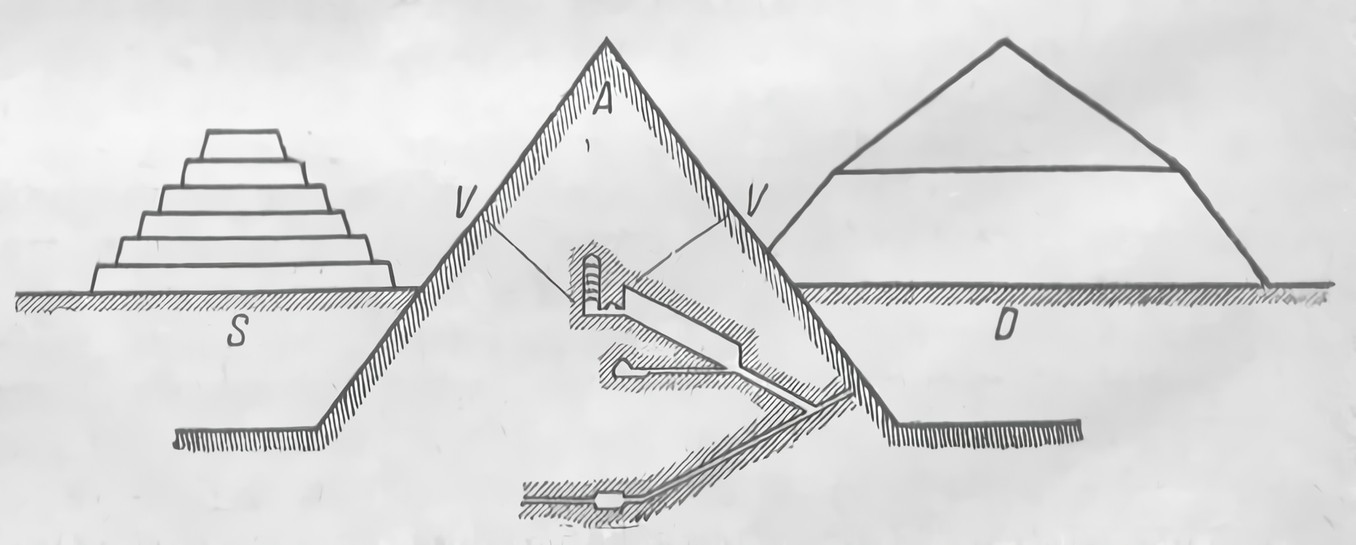
Рис. 11. Египетские пирамиды

 

 

Оба эти явления поставили с необыкновенной остротой проблему статики всего сооружения в целом и заставили искать способов предварительного расчета пропорций между шириной и высотой постройки.

 

Чисто эмпирически найденный и грубо практически применявшийся профиль равного сопротивления обратил внимание строителей на треугольник, которым и стали класть в основу профиля сооружения (рис. 12). В Египте для построения этого треугольника пользовались двумя «египетскими» треугольниками со сторонами 3, 4, 5. Их применяли в различных комбинациях: их складывали то большими, то меньшими катетами, или же применяли разнообразные сочетания сторон этих треугольников. На той же основе строили и профили сводов, описывая их из трех центров: из углов, прилежащих основаниям, радиусами, равными длине этого последнего, и из вершины большого треугольника, радиусом, равным разности между основанием и стороной большего треугольника.

 

 

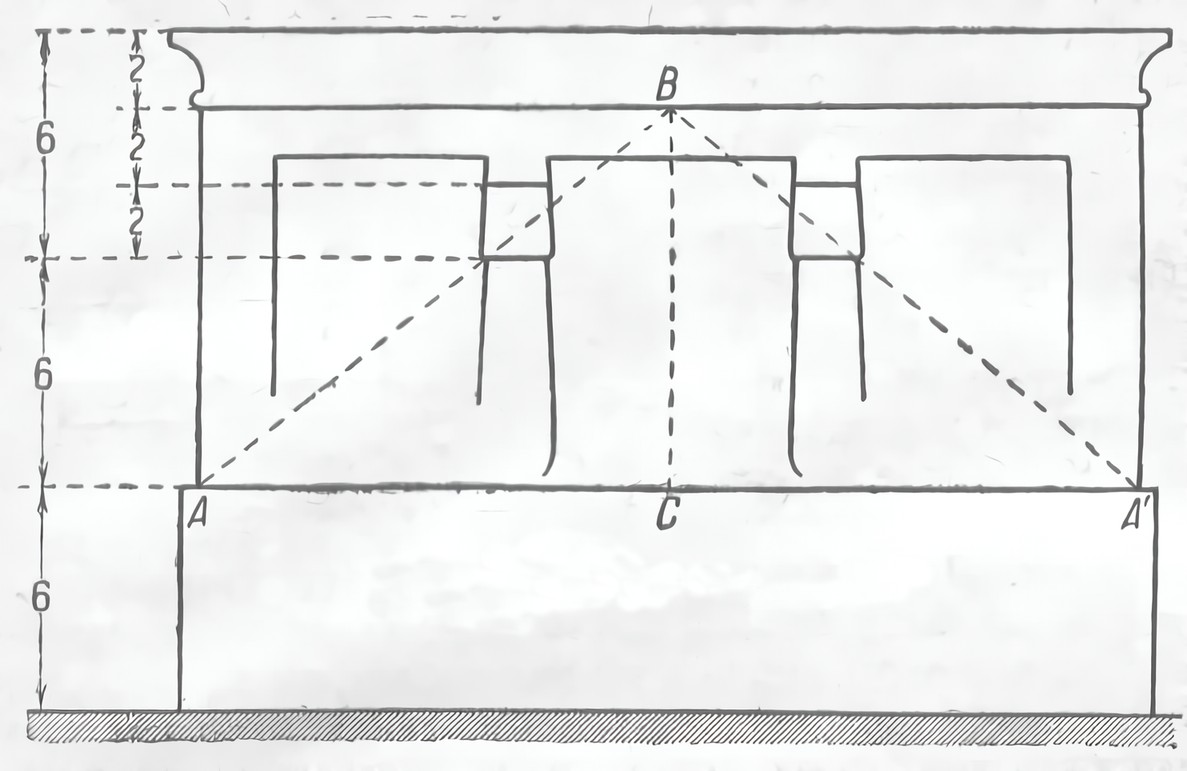
Рис. 12. Профиль фасада египетского храма

 

 

Но искания наиболее эффектных решений натолкнули на другие пропорции — это были равносторонний треугольник и гармоническая пропорция, известная также под названием «золотого сечения» (рис. 13). Оба они были открыты и изучены в связи с анализом геометрии окружности, которая привлекла внимание математиков в связи с работой над проблемами астрономии. Деление окружности путем вписывания в нее правильных многоугольников привело к изучению равностороннего треугольника и звездчатого пятиугольника — пентаграммы. Равносторонний треугольник был продуктом работы над правильным шестиугольником, который привлекал внимание математиков тем, что его сторона равнялась радиусу описанной окружности, а сам он был геометрической основой шестидесятеричной системы исчисления, разработанной халдейскими астрономами и до сих пор удержавшейся в мерах времени и окружности. Равносторонний треугольник получался в результате соединения через один углов правильного шестиугольника. Тем же путем из правильного выпуклого пятиугольника получалась пентаграмма. Пятиугольник, образуемый сторонами выпуклого пятиугольника и пентаграммы, давал как раз «золотое сечение». То же самое давал треугольник, высота которого определялась делением основания в гармоническом отношении или, как иначе говорили, в крайнем и среднем отношении.

 

 

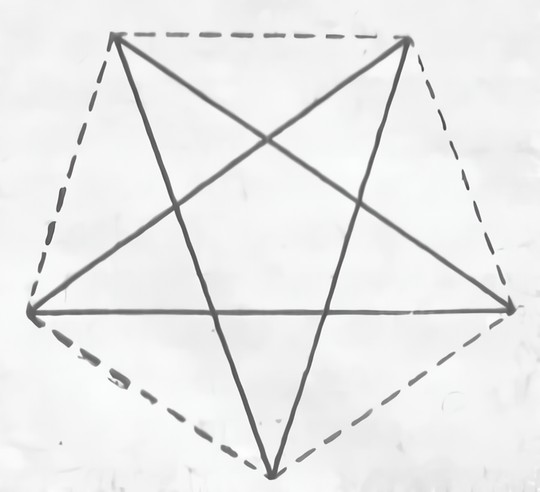
Рис. 13. Звездчатый пятиугольник

 

 

Не меньшее значение имели пропорции отдельных частей сооружения: соотношения длины и высоты архитрава, высоты и толщины колонны, длины колонны и высоты антаблемента, высоты базы и капители. За основу всех этих расчетов были взяты определенные модули, обусловленные конструктивными элементами сооружения. В одних случаях это была длина кирпича или каменного блока, в других — радиус колонны. И всем соотношениям было дано числовое выражение в виде пропорций.

 

Проблема пропорций имела не только конструктивное значение. Характерное для третьей стадии варварства превращение архитектуры в искусство и разделение уже в эпоху цивилизации общества на классы, превратило архитектуру в колоссальной силы орудие идеологического воздействия, а господствующие классы пользовались им как орудием угнетения. Стремление жрецов и царей оказать возможно большее воздействие на психику населения архитектурой храмов и дворцов толкнуло архитекторов на поиски наиболее красивых пропорций и привело к воспроизведению некоторых пропорций человеческого тела¹, в частности соотношения роста и длины головы, роста и ступни.

____________

¹ Витрувий, кн. III, стр. 6.

 

Архитектурные расчеты явились стимулом и исходной точкой колоссального развития математического учения о пропорциях. Во время своих путешествий Пифагор познакомился на Востоке с египетским треугольником, который пользовался широким применением у архитекторов и землемеров, так как давал им возможность при помощи веревки с узлами строить прямой угол, бывший основной формой углов зданий и земельных участков. Исследуя соотношение сторон всевозможных прямоугольных треугольников, Пифагор установил свою знаменитую теорему. Он же разработал и учение о пропорциях, так необходимое для архитектуры. Техника строительного дела нашла отражение в работах пифагорейцев еще и в другом отношении. Утверждение, что часть плоскости, расположенная вокруг точки, может быть совершенно заполнена шестью равносторонними треугольниками, четырьмя квадратами или тремя правильными шестиугольниками, и теория, что пространство вокруг точки заполняется правильными телами — тетраэдром, октаэдром, кубом и икосаэдром, — представляли собой продукт математической обработки данных тогдашней техники строительного дела, в особенности богатый материал в этом отношении давала полигональная кладка.

 

Вскоре выяснилось, что с равнобедренным треугольником, катеты которого равны единице, не все обстояло благополучно. Сумма квадратов, построенных на его катетах, равнялась, как и в других треугольниках, квадрату, построенному на гипотенузе. Но сумма соответствовавших катетам квадратных чисел 1 и 1 оказывалась числом не квадратным. Она равнялась 2. Другими словами, это число, как выразились пифагорейцы, не имело стороны и не могло выразить прямой линии в такой простой фигуре, как равнобедренный прямоугольный треугольник.

 

Таким образом у пифагорейцев сложилось понятие о несоизмеримых иррациональных величинах, отношение которых было невозможно выразить никаким конечным числом — ни целым, ни дробным. А между тем древнегреческая математика никаких других чисел кроме конечных не знала. Для нее число было конечной совокупностью единиц или равных частей единицы. Это обусловливалось общим духом идеологии консервативного рабовладельческого общества. Она была проникнута механическим и статическим пониманием окружающего. Античное сознание рассматривало все вещи изолированно друг от друга и в состоянии — одну без другой, одну после другой.

 

Еще большую остроту проблема несоизмеримости приобрела в связи с работой над задачей определения площади круга, возникшей под влиянием выведения надстроек, круглых в плане. В Египте такую форму имели, например, житницы.

 

Работа над этой задачей привела Антифона, математика V столетия до начала современного летоисчисления, к открытию метода истощения. Вписав в окружность квадрат, он построил на его сторонах равнобедренный треугольник и продолжал так до тех пор, пока не получил (рис. 14) многоугольника, стороны которого почти совпадали с окружностью. Таким образом круг как бы истощался. Однако неполное истощение круга заставило его современника Бризона Гераклейского применить кроме вписанного многоугольника еще и описанный и принять площадь круга за среднее арифметическое между этими двумя площадями.

 

 

Рис. 14. Антифоново решение задачи квадратуры круга

 

 

Проблема квадратуры круга вызвала большие споры философского характера, наложившие печать на все развитие математики вплоть до Декарта.

 

Против методов Антифона и Бризона математики возражали указанием на то, что идея совпадения многоугольника с кругом противоречит представлению, что величины делимы до бесконечности. С математиками в этом вопросе расходились философы. Один из руководителей элейской школы Зенон доказывал, что прямая линия и кривая в конце концов приводятся к одним и тем же неделимым элементам. В доказательство своей идеи Зенон ссылался на то, что в противном случае быстроногий герой гомеровских произведений Ахилл не мог бы догнать черепахи, так как, на какое бы расстояние он ни продвинулся, черепаха все равно за это время тоже продвинулась бы вперед. Он указывал еще и на то, что если правы его противники, то и «летающая стрела находится постоянно в покое, потому что в каждый момент она находится только в одном месте».

 

Здесь античные математики подошли к одному из важнейших вопросов философии — вопросу о бесконечности.

 

Проблемы бесконечного касался и великий философ древности, автор атомистики, Демокрит. Если конус «разрезать плоскостями, — говорит, по утверждению Плутарха, Демокрит, — параллельными основанию, то что следует думать о площадях отрезков: будут ли они равны или неравны? Если они неравны, то они делают конус негладким, имеющим множество выступов и углублений наподобие лестницы. Если же допустить, что отрезки равны, то окажется, что конус имеет свойство цилиндра, состоя из равных, а не неравных кругов, что крайне нелепо»1. Самая эта идея, впоследствии положенная математиками XVII в. в основу анализа бесконечно малых, была подсказана строительной техникой — лестничной кладкой и кладкой напуском. Недаром Демокрит был автором теории свода. Очень возможно, что кладка в известной мере подсказала ему и его философскую концепцию.

____________

¹ Кэдэкорн, История элементарной математики, стр. 329.

 

«Бесконечность, — пишет Энгельс, — это противоречие, и она полна противоречий. Противоречие заключается уже в том, что бесконечность должна состоять исключительно из конечных величин, а ведь на деле оно так и есть²». Уже простое механическое движение в пространстве может происходить лишь так, что тело в один и тот же момент пребывает в одном месте и в то же время в другом»³.

____________

² «Анти-Дюринг», стр. 45.

³ Там же, стр. 109.

 

«Математика, говоря о бесконечно большом и бесконечно малом, вводит количественное различие, принимающее даже вид неустранимой качественной противоположности. Количества, которые так колоссально отличны друг от друга, что между ними прекращается всякое рациональное отношение, всякое сравнение, становятся количествами несоизмеримыми. Обычная несоизмеримость круга и прямой линии является диалектическим качественным различием, но здесь именно количественное различие однородных величин возвышает качественное различие до несоизмеримости»⁴.

____________

⁴ Там же, стр. 33.

 

Для того чтобы понять это, надо было быть диалектиком. Но этого не могли понять греческие математики. Вместо того, чтобы анализировать эти противоречия, они изгнали из своей науки противоречивое понятие о бесконечно малом и бесконечно большом и ввели строгое логическое доказательство даже совершенно очевидных теорем, вроде теоремы о том, что два пересекающиеся круга не могут иметь общего центра. Математическая наука стала развиваться по пути максимальной логической строгости формулировок и доказательств, но в то же самое время по пути метафизической, идеалистической методологии.

 

Логическая обработка математики была выполнена философом V—IV вв. до начала современного летоисчисления Платоном. Он начал давать тщательные с логической стороны определения, ввел постулаты и аксиомы, которые, не требуя доказательств в силу своей очевидности, являлись логическими посылками для доказательства всех теорем и разрешения всех проблем. Он определил тело, как нечто, имеющее три измерения, точку — как «начало прямой линии», ее границу или как «неделимую линию». Линию Платон определял как границу поверхности, плоскость — как границу тела. Короче говоря, он начал исследовать формы и отношения в их чистом виде и в их рациональной связи между собой.

 

«Для того же, — пишет Энгельс, — чтобы эти формы и отношения исследовать в чистом виде, необходимо отделить их от их содержания и последнее как безразличное отбросить, тогда мы получаем точки без протяжения, линии без толщины и ширины. Кажущееся выведение одних математических величин из других доказывает не их априористическое происхождение, а только их рациональную связь между собой»⁵.

____________

⁵ Там же.

 

Вот эту-то работу и проделал Платон. А его продолжатели стали рассматривать математические построения независимо от реального мира, откуда они были взяты, рассматривать их как «свободные создания и измышления разума». Здесь проявилось то, о чем, критикуя Дюринга, говорит Энгельс:

 

«Во всех областях мысли, заимствованные из реального мира, законы на известной ступени развития обособляются от действительного мира и противопоставляются ему как нечто самостоятельное, как приходящие извне законы, которым мир должен подчиняться»¹.

____________

¹ «Анти-Дюринг», стр. 33.

 

Анализируя дальше связь чистой математики с реальным миром, Энгельс указывает, что «чистая математика была впоследствии приложена к миру, хотя она взята именно из этого мира, и образует лишь часть его составных форм, и только поэтому она вообще находит себе применение».

 

Греческие математики не только игнорировали такое происхождение математики, но и отрицали необходимость ее практического применения. Пифагору приписывают, будто он гордился тем, что «поставил арифметику выше потребностей торгаша». Платон писал: «Утвердим законом, чтобы упражнялись в науке счисления не для купли и продажи, а входили мыслью в созерцание чисел с целью облегчить душе обращение от вещей преходящих — к истине и вечной сущности»². Для землемерия и военного дела, по его словам, «было бы достаточно небольшой части арифметики и геометрии: их большая и главная часть имеет целью способствовать познанию блаженного вечно сущего». Про Эвклида сообщают, как в ответ на вопрос одного из своих учеников «Что я приобрету, изучая эти вещи?» он позвал своего раба и сказал ему: «Дай ему три обола, — он хочет, чтобы учение приносило ему прибыль».

____________

² Лоренц, Элементы высшей математики, изд. Сытина, 1903 г., т. I, стр. 129.

 

Такой взгляд был результатом того, что производство держалось на рабском труде, вследствие чего, как говорит Энгельс, «всякая производительная работа считалась рабским трудом, недостойным свободного римлянина (и грека)», и господствовало «презирание производительного труда свободными людьми»³.

____________

³ Энгельс, Происхождение семьи, изд. 1894 г., стр. 146.

 

Громадную роль строительное дело сыграло также в постановке и второй великой геометрической задачи древности: задачи удвоения куба.

 

Постройка храмов, в которых жертвенники делались кубической формы из соображений религиозного характера, поставила перед каменщиками техническую проблему — найти способ удвоения куба⁴. Из кладки кубических алтарей им было известно в грубых чертах соотношение между ребрами данного и удвоенного куба. Это соотношение они применяли для своих практических надобностей. Однако за решение задачи вскоре взялись геометры. Это было обусловлено тем, что они помимо своего сознания и желания являлись по существу теоретиками строительного дела. Конечно, геометры придали задаче отвлеченно математическую постановку и формулировку. Однако их работа по сути свелась к обобщению наблюдений ремесленников. В то время считали возможным решать геометрические задачи только путем построения и притом лишь с помощью циркуля и линейки. Это обстоятельство было обусловлено технической ролью геометрии. Она являлась средством решения вопросов землемерия и архитектуры. Решение же этих технических задач сводилось к построению чертежей, по которым затем уже и выполнялась работа.

____________

⁴ Следы такого именно происхождения этой задачи сохранились в известной легенде о том, что ее поставил дельфийский оракул в ответ на вопрос, каким образом «прогнать чуму». Его совет — удвоить жертвенник в храме Аполлона, пытались выполнить как удвоением ребра куба, так и удвоением высоты куба. На недоуменный вопрос, почему же не прекращается чума, оракул в легенде отвечает — потому что вы не знаете божественной науки — геометрии. Отсюда и самая задача известна под именем делосской или дельфийской.

 

Понятие о телах вращения, частным случаем которых является конус, сложилось не в результате досужего созерцания природы. Основу его составила практика ремесленников-гончаров, которые пользовались при изготовлении посуды в качестве станка вращающимся деревянным кругом. Представление же о конических сечениях возникло в результате отрезывания от конуса сырой глины частей и кусков лишних с технической точки зрения. Гончарный круг широко применялся еще в древней Греции, и это обстоятельство для исканий и достижений греческих геометров сыграло громадную роль. Вырабатывая научные понятия тела вращения, круглого конуса и конических сечений, они бессознательно обобщили техническую практику ремесленников.

 

Научно первый поставил ее Гиппократ из Хиоса, греческий геометр-педагог V в. до начала современного летоисчисления. Он показал, что для ее решения следует найти первое из двух средних пропорциональных между ребром данного куба и линией вдвое большей длины.

 

Итак, по причинам, изложенным выше, задачу удвоения куба нужно было решать при помощи построения. А между тем известные тогда геометрические места — прямая и окружность — были бессильны дать требуемое решение. Создалось противоречие. Имелась налицо определенная научная потребность, наличных же средств оказалось недостаточно для ее решения. Вот это противоречие и выдвинуло перед греческими геометрами IV—III вв. теоретическую задачу отыскания и изучения новых геометрических мест.

 

Конические сечения привлекли внимание геометров, потому что окружность была тоже одной из кривых этого рода. Она получилась при срезывании верхушки конуса по плоскости, параллельной его основанию. Понятие конических сечений было к тому времени уже выработано практикой гончарного дела. Таким образом геометрам оставалось изучить основные свойства этих кривых. Они стали выяснять их, отыскивая соответствия с известными им свойствами окружности.

 

Первые шаги в этом направлении были сделаны геометром IV в. Менейхмом. Со времени Пифагора математики знали свойства перпендикуляра, опущенного из какой-либо точки окружности на ее диаметр. Он являлся средним пропорциональным между отрезками диаметра. При помощи такого построения греческие геометры решали неполные квадратные уравнения и четырехчленные пропорции. Это и навело Менейхма на поиски подобных же отношений в других конических сечениях. На этом пути он искал способа построить пропорцию Гиппократа.

 

Пересекая три вида конуса: прямоугольный, остроугольный и тупоугольный, плоскостью, перпендикулярной к их образующей, Менейхм получил три кривые (рис. 15). Для каждой из этих кривых соотношение элементов, аналогичных диаметру окружностей и опущенному на него перпендикуляру, было различно. Оно было выражено Менейхмом в форме трех теорем.

 

 

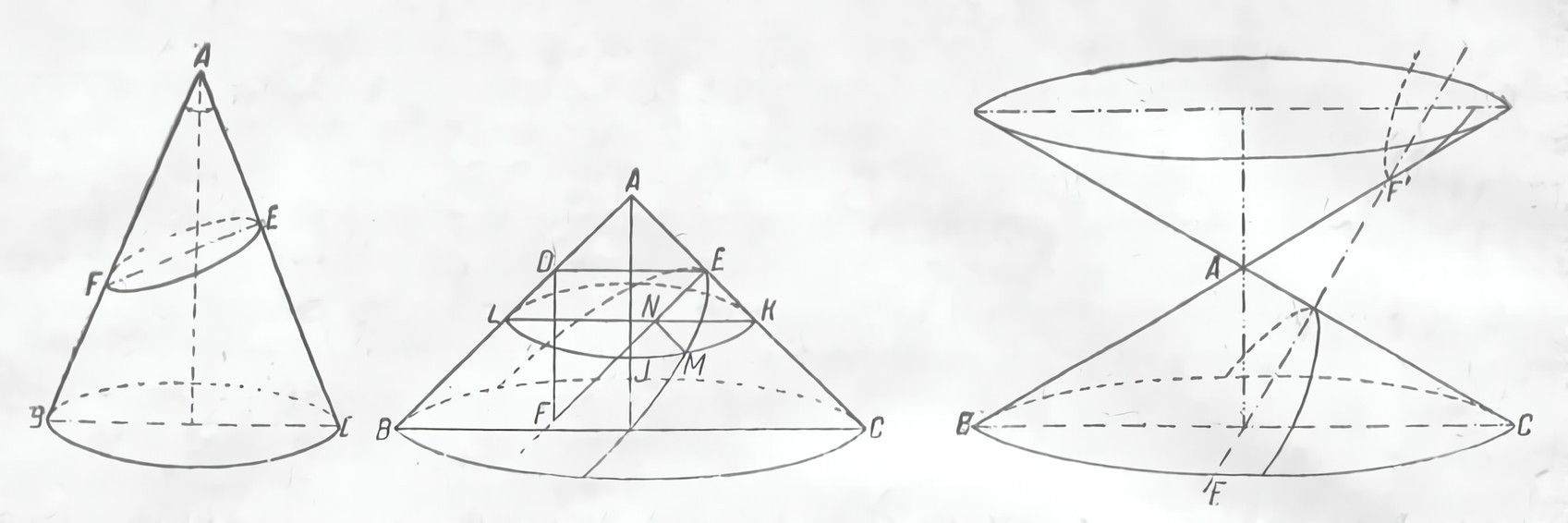
Рис. 15. Конические сечения Менейхма

 

 

В сечении прямоугольного конуса это отношение оказалось очень простым. Квадрат, построенный на перпендикуляре, был равновелик прямоугольнику, образованному из отрезков оси симметрии. Для двух других кривых зависимость оказалась гораздо сложнее. Там было взято отношение площади квадрата, построенного на перпендикуляре, к площади прямоугольника, образованного двумя отрезками оси. При помощи сечения прямоугольного и тупоугольного конуса Менейхм решил задачу об удвоении куба (рис. 16), которая собственно и толкнула математиков на поиски и изучение новых геометрических мест.

 

 

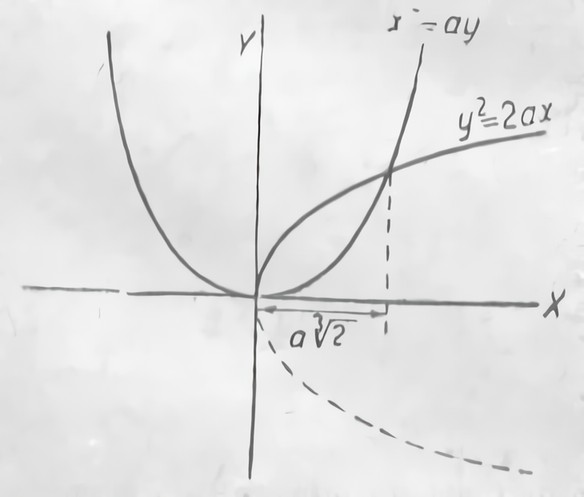
Рис. 16. Решение Менейхмом задачи удвоения куба

 

 

Геометры глубоко заинтересовались свойствами этих кривых и стали изучать их независимо от их практических применений.

 

Постепенно находились все новые и новые свойства. К концу IV в. учение о конических сечениях состояло уже из большого количества положений, не имеющих между собой никакой логической связи. Это обстоятельство сильно затрудняло пользование кривыми как в научно-педагогической, так и в в научно-исследовательской практике. И учащимся и исследователю было трудно запомнить все отдельные, не связанные между собой, их свойства. Отсюда-то и выросло стремление к систематизации всего материала, накопленного в течение десятилетий.

 

Первым шагом в деле решения этой задачи было составление двух сводов.

 

Один из сводов был составлен знаменитым геометром-систематизатором III в. Эвклидом. Четыре книги Эвклида о конических сечениях не сохранились до нашего времени, и поэтому их содержание осталось нам неизвестным.

 

Гораздо более глубоко и последовательно эту задачу систематизации решил ученик Эвклида — геометр III и II вв. Аполлоний из Перги. В своих восьми книгах он изложил учение о конических сечениях с более общей точки зрения, чем его предшественники, и значительно строже в отношении систематичности.

 

Вместо конуса Аполлоний брал более общий вид конической поверхности (рис. 17). Она была образована движением по окружности конца прямой, середина которой проходила через неподвижную точку. Эта точка лежала вне плоскости данной окружности. На такой конической поверхности Аполлоний получал все три кривые путем простого изменения угла между образующей и секущей плоскостями. Сечение прямоугольного конуса получалось, когда этот угол равнялся углу при вершине конуса. Остроугольное сечение образовывалось, когда первый угол был меньше второго, а тупоугольное в том случае, если он был больше. Таким образом Аполлоний показал, что величина угла при вершине сама по себе не имеет значения. Вид же кривой определяется соотношением общих указанных выше углов.

 

 

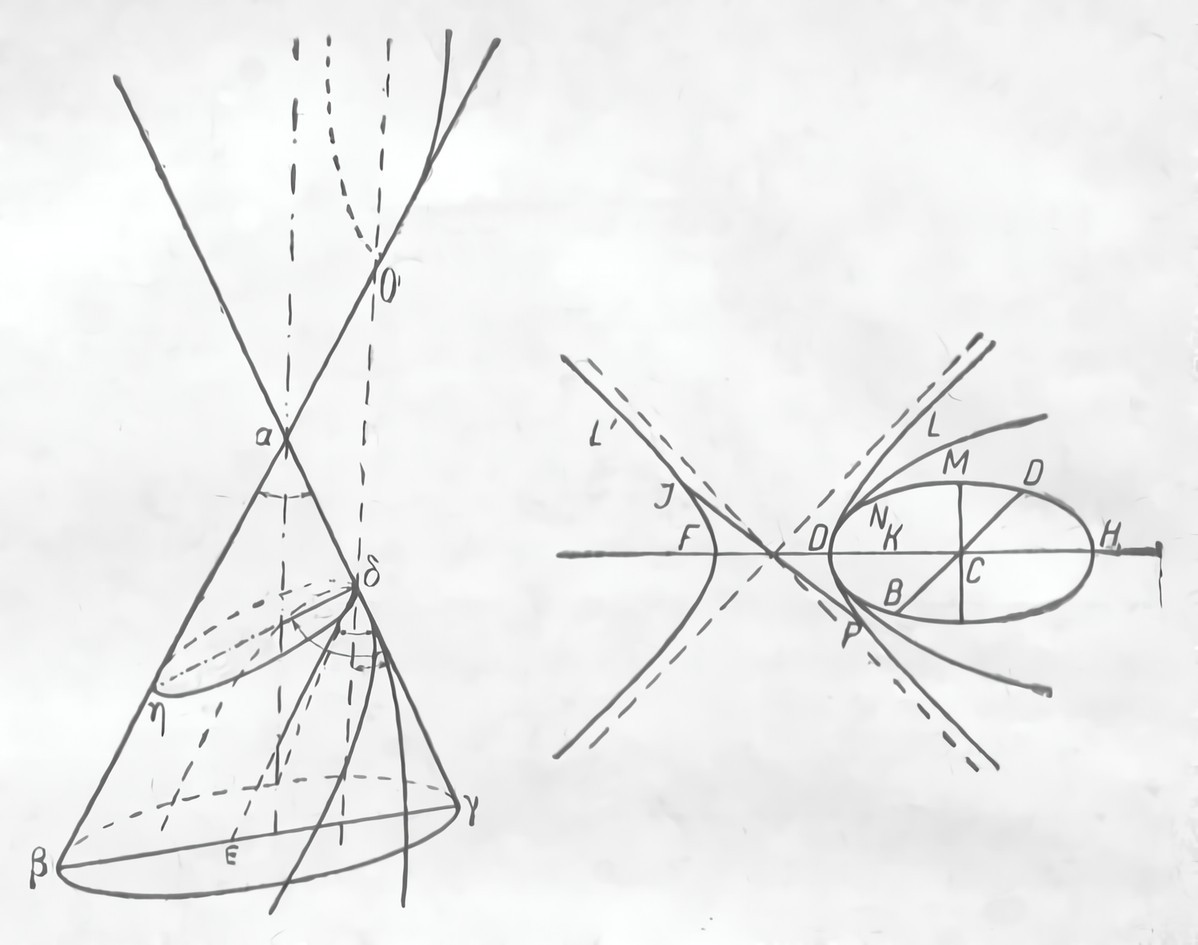
Рис. 17. Построение Аполлония

 

 

Конические сечения Аполлоний изучал теми же методами, что и Менейхм. Для всех трех кривых он установил отношение квадрата, построенного на перпендикуляре, который опущен из любой точки сечения на его ось, к прямоугольнику, образованному отрезком оси от основания перпендикуляра до вершины кривой и ее параметром. В первой кривой эти площади оказались равновеликими, поэтому Аполлоний назвал ее параболой, т. е. равенством. Для второго сечения площадь квадрата была меньше площади прямоугольника. Отсюда ей было дано название эллипса, что значит недостаток. Наконец, в последней кривой площадь квадрата являлась большей. Поэтому она была названа гиперболой, т. е. избытком.

 

Третья великая геометрическая задача древности — проблема деления угла на три равные части — была связана с градуированием окружности, имевшим огромное значение и для строительного дела. Разделить окружность на градусы по шестидесятеричной системе было совершенно невозможно без умения делить любой угол на три части. Большую роль в разработке этой проблемы сыграло также построение правильных многоугольников, при помощи которых долгое время изучали геометрию круга. С частным решением для прямого угла справились уже пифагорейцы, делившие прямой угол при помощи равностороннего треугольника (рис. 18). Но общее решение доставило затруднение не меньше, чем задача удвоения куба. В поисках решения геометры открыли новые геометрические места. Греческий философ и математик Гиппий из Элиды в V в. до начала современного летоисчисления открыл таким образом квадратриксу (рис. 19), а его младший современник Никомед — конхоиду (рис. 20). Пытались применять для решения этой задачи и конические сечения. Папа Александрийский воспользовался для этой цели гиперболой. Таким образом строительное дело непосредственно и через посредство механики оказало влияние на развитие античной математики.

 

 

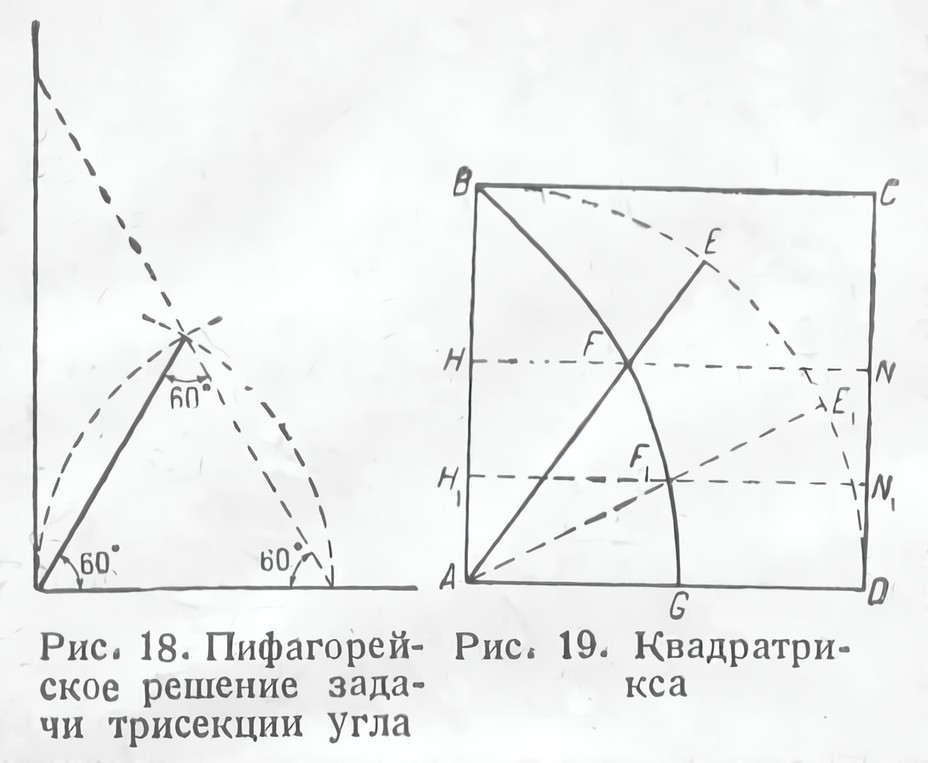
Рис. 18. Пифагорейское решение задачи трисекции угла

Рис. 19. Квадратрикса

 

 

 

«Архитектура, — пишет Витрувий, — есть такая наука, с которой должно сопряжено быть множество других различных наук и знаний. Архитектор должен знать писать и рисовать, искусен быть в арифметике и в геометрии, знающий, также в оптике. Гораздо знать историю и хорошо философию, а сверх того надобно еще ему иметь понятие о музыке, и знать хоть слегка врачебную науку, юриспруденцию и астрономию. Все сии знания архитектору необходимо надобны для следующих причин. Чтобы не позабыть, что ему надобно делать, должен он иметь порядочные записки, и для того знать хорошо писать. Должен знать рисовать, дабы способнее мог по сделанным рисункам... производить в дело здания, которые он предпринимает. Геометрия великую подает ему помощь, а особливо она научит его, как употреблять с пользою линейку и циркуль, как вести строение по прямым и порядочным чертежам и возвышать стены по наугольнику и ватерпасу. Оптика ему покажет, как окошки порядочнее расстановлять и свет строению давать по расположению неба. Арифметика служить ему будет к исчислению денег, потребных на строение зданий, которые он берется делать, и к утверждению мер и пропорций, которые часто находятся лучше по исчислению, нежели по геометрии. История, дает ему материю большей части украшений архитектурных, которых должен он знать причину. Та часть философии, которая рассуждает о естественных вещах и по-гречески называется фисиологией, сделает его способным к решению многих задач: что ему весьма нужно во многих случаях, как-то, например, в провождении вод. Кроме того, архитектору без знания философии никогда не можно будет разуметь того, что написано в книгах Ктезибия, Архимеда и других подобных писателей. Что же касается до музыки, то в ней архитектор должен быть совершенно знающим: ибо без оной не может он знать пропорции канонической и математической в натягивании надлежащим образом орудий военных. Знание музыки нужно еще к пристойному расстановлению сосудов медных, которые становятся под ступенями театральными по математической пропорции и по свойственному им различию звука. Надобно также архитектору иметь понятие о врачебной науке, ежели он хочет знать разные положения мест или стран земных, что греки называют клима́та, чтобы по тому спознал он качество воздуха, здоров он или вреден, и какие суть разные свойства, вод. Архитектор должен еще знать юриспруденцию или законы и обыкновения разных мест для строения соседственных стен, для расположения стоков и отходных мест, для распространения вида в каждом строении и для стечения воды... Астрология также будет способствовать архитектору к делению солнечных часов помощью того знания, которое она подает ему о востоке, о западе, о юге и о севере, также о равнонощиях, о поворотах солнца и обо всем течении звезд.

 

Может быть, невеждам покажется непонятно, чтобы разум и память одного человека могли снискать столь многие знания, но ежели они приметят, что все науки имеют сообщение и связь между собою, то уверены будут о сей возможности... И кто учился с молодых лет, тот легко сие узнает из сходственностей, которые ему встречаются между некоторыми общими всем наукам вещами, из коих одна служит к удобнейшему познанию другой»¹.

____________

¹ Витрувий, кн. I, стр. 43.

 

 

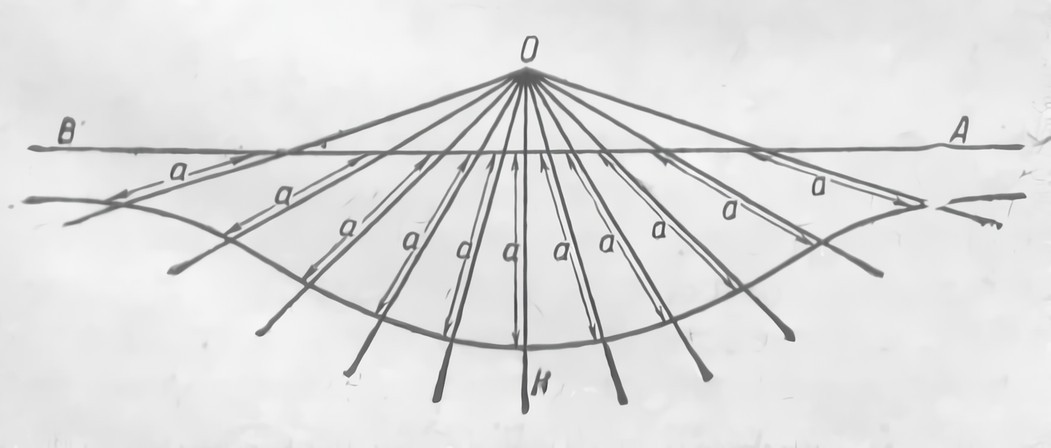
Рис. 20. Конхоида

 

 

Каждая эпоха имеет свои ведущие отрасли техники, специалисты которых являются наиболее типичными представителями техники данной эпохи. Эпоху второго великого общественного разделения труда лучше всего представляет архитектор.