|
|
Хэмбидж Д. Динамическая симметрия в архитектуре. — Москва, 1936  Динамическая симметрия в архитектуре / Д. Хэмбидж ; Перевод с английского В. Белюстина ; Под редакцией Н. Брунова ; Предисловие и примечания Ю. Милонова. — Москва : Издательство Всесоюзной Академии архитектуры, 1936. — 200, [3] с. : ил. — (Архитектурные пропорции; Выпуск III).[Оригинальное название на английском]
PRACTICAL APPLICATIONS OF DYNAMIC SYMMETRY
THE PARTHENON AND OTHER GREEK TEMPLES
THEIR DYNAMIC SYMMETRY
by JAY HAMBIDGE
ПРЕДИСЛОВИЕ
Выделение из всей сложной и многогранной проблемы архитектурных пропорций вопроса о том, какими математическими приемами строили их мастера той или другой эпохи, является, конечно, чрезвычайно односторонним подходом. Такой подход не может объяснить ни корней возникновения и преобладания именно данных, а не иных соотношений, ни причин их эстетического воздействия на зрителей. Но с точки зрения архитектора, которого занимают технические приемы мастеров прошлого, он интересен точно так же, как для математика интересны приемы средневекового счета, а для лингвиста история грамматики. Вот этой-то грамматике архитектурных пропорций и посвящена книга американского искусствоведа Хэмбиджа.
Автору кажется, будто он вновь нашел тот метод построении архитектурных пропорций, который применяли античные греки, но который был утерян свыше двух тысяч лет тому назад.
Утверждение ученика греческих мастеров, римского теоретика Витрувия, что эти пропорции строились при помощи определенного модуля, выражавшего соизмеримые отношения части сооружения к целому, Хэмбидж считает не соответствующим действительности. Доказательство этому он видит в том, что обмеры греческих зданий дают соотношения, не совпадающие с канонами Витрувия, и наоборот, обнаруживают наличие несоизмеримых величин.
Ему представляется, что недоуменный вопрос о том, как могли рабочие при таких условиях производить свои работы, становится ясным только после отказа от принципа соизмеримости отрезков линии и замены этого последнего принципом соизмеримости элементов площадей. Наиболее ярким выражением такого метода Хэмбидж считает знаменитую теорему Пифагора.
В обосновываемом им принципе динамической симметрии Хэмбидж исходит из одного отрывка из платоновского „Теэтета“.
„Феодор, — говорится в этом отрывке, — объяснял нам чертежами нечто о потенциях, о трехфутовой и пятифутовой величине, доказывая, что по долготе они несоразмерны футу; так брал он каждую порознь потенцию до семнадцатифутовой и на этой как-то остановился. Тогда пришло нам в голову нечто подобное твоему вопросу: так как потенций представлялось бесчисленное множество, то нам вздумалось попытаться заключить их в одной, чтобы этою одною обозначить все потенции ... Всякое число мы разделили на-двое и ту его часть, которая могла быть равножды равною, уподобив четвероугольнику, назвали равносторонним четвероугольником ... , а число промежуточное, как, например, три, пять и всякое, которому нельзя быть равножды равным, но которое бывает корнем произведения или большего на меньшее или меньшего на большее и за свои стороны всегда принимает большее и меньшее, такое число, уподобив опять фигуре продолговатой, мы назвали числом продолговатым ... Все линии, изображающие число равностороннего четвероугольника и четвероугольной плоскости, мы определили понятием долготы, а все дающие число из различных протяжений — понятием потенций, так как по долготе эти числа соразмерны не тем, а плоскостям, на которые указывают“ (сочинения Платона, переведенные с греческого и объясненные профессором Карповым. Синод. типография, 1876).
Смысл этого места платоновского „Теэтета“ сводится в переводе на язык современной математики к следующему. Речь идет об общем способе выражения квадратных корней как рациональных, так и иррациональных. Если какое-нибудь число поддается разложению на два равные друг другу множителя, то его корень является величиной рациональной, если же его можно разложить только на два неравных множителя, то корень представляет собой величину иррациональную. Геометрически первое произведение может быть выражено квадратом, второе же лишь удлиненным прямоугольником. Квадрат может быть определен величиной любой из его сторон. Прямоугольник же определяется двумя его сторонами, характеризующими всю его поверхность.
Исходя из этого отрывка и теоремы Пифагора, Хэмбидж строит свою систему динамической симметрии следующим образом. Он проводит в квадрате диагональ, которая относится к стороне квадрата как
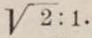 По пифагоровой теореме квадрат, построенный на этой диагонали, вдвое больше исходного квадрата. На этой диагонали и стороне квадрата он строит прямоугольник По пифагоровой теореме квадрат, построенный на этой диагонали, вдвое больше исходного квадрата. На этой диагонали и стороне квадрата он строит прямоугольник  . Затем снова проводит диагональ в этом новом прямоугольнике. Построенный на ней квадрат равен сумме квадратов, построенных на большей и меньшей сторонах прямоугольника . Затем снова проводит диагональ в этом новом прямоугольнике. Построенный на ней квадрат равен сумме квадратов, построенных на большей и меньшей сторонах прямоугольника  Но квадрат, построенный на большей стороне, вдвое больше квадрата, построенного на меньшей стороне этого прямоугольника. Это значит, что квадрат новой диагонали втрое больше первичного квадрата или, что то же самое, квадрата меньшей стороны прямоугольника. Она относится к высоте прямоугольника как Но квадрат, построенный на большей стороне, вдвое больше квадрата, построенного на меньшей стороне этого прямоугольника. Это значит, что квадрат новой диагонали втрое больше первичного квадрата или, что то же самое, квадрата меньшей стороны прямоугольника. Она относится к высоте прямоугольника как  Взяв ее за основание, а высоту оставив прежней, можно построить новый прямоугольник Взяв ее за основание, а высоту оставив прежней, можно построить новый прямоугольник  Точно так же он строит прямоугольники Точно так же он строит прямоугольники  и и  Квадрат основания первого из них вчетверо больше, а квадрат основания второго впятеро больше исходного квадрата. Построение это может быть продолжено до бесконечности. Квадрат основания первого из них вчетверо больше, а квадрат основания второго впятеро больше исходного квадрата. Построение это может быть продолжено до бесконечности.
Площадь исходного квадрата Хэмбидж считает выражением статической симметрии, потому что это правильная геометрическая фигура. Наивысшим выражением динамической симметрии он считает прямоугольник
 Площади же прямоугольников Площади же прямоугольников  он рассматривает как промежуточные ступени между статической и динамической симметрией. он рассматривает как промежуточные ступени между статической и динамической симметрией.
Такова в своих основных чертах точка зрения Хэмбиджа.
Действительно ли она восстанавливает подлинные методы греческих зодчих, утерянные уже в эпоху Витрувия?
Действительно ли модульный метод, излагаемый Витрувием, противоречит представлениям греческих строителей эпохи расцвета?
У того же Платона, на которого ссылается Хэмбидж, есть совершенно недвусмысленные указания, как представляли себе в его время пропорции зданий и сооружений вообще. Эти указания содержатся в описании воображаемой стены Атлантиды. „Храм самого Посейдона, — пишет он в „Критии“, — имел одну стадию в длину, три плетра в ширину и пропорциональную ему на вид высоту“. Тот же самый прием Платон применяет, описывая равнину, на которой расположен главный город атлантидян. „В основании, — говорит он про историю планировки местности, — лежал большей частью правильный и продолговатый четвероугольник, а чего недоставало (для такой формы), то направляемо было по окружности выкопанного кругом рва. Показания относительно его глубины, ширины и длины невероятны, — [невероятно], чтобы сверх других произведений труда, было еще такое, созданное руками, дело; но передадим, что слышали. В глубину был он прокопан на один плетр, в ширину повсюду на одну стадию и так как был выкопан кругом всей равнины, то оказался до десяти тысяч стадий в длину“. Таким же образом Платон определяет и размеры канала, идущего к царскому дворцу: „Начиная от моря вплоть до крайнего внешнего кольца прокопали они канал в три плетра ширины и сто футов глубины, длиною же в пятьдесят стадий“.
Таким образом, представления о пропорциях здания у Платона гораздо ближе к представлениям Витрувия, чем к схемам Хэмбиджа.
Современные обмеры, данные которых Хэмбидж считает вполне надежной исходной точкой для своих математических выкладок, на самом деле не являются уже таким надежным фундаментом для точных вычислений. Здесь нельзя игнорировать те деформации, которые произошли на протяжении тысячелетий и в материале и в здании в целом. Осадка и выветривание сильно изменили первоначальные пропорции. Так, например в Парфеноне, который служит Хэмбиджу основным объектом, целые пласты стилобата сползли со своих первоначальных постелей и тем самым сильно изменили его первоначальный наружный вид. Относительно высоты пирамиды Хеопса известно, что она под влиянием выветривания облицовки на протяжении одного столетия значительно уменьшилась. Этих вековых деформаций не учитывает Хэмбидж, а между тем очень возможно, что во многих случаях именно ими и объясняется та несоизмеримость частей, которая так удивляла археологов.
Наконец, Хэмбидж совершенно не считается с неизбежными погрешностями измерения. Тут громадную роль играют и степень натяжения рулетки, и влажность воздуха, и даже его температура. Под влиянием этих факторов деформируется эталон измерения, а вместе с тем и результаты обмера. Ведь существуют же значительные расхождения между всеми авторами, производившими обмеры Парфенона — Стюартом, Колиньоном, Пенрозом. Поэтому точность до тысячных долей фута, с которой оперирует Хэмбидж, совершенно бессмысленна.
В математике существует целая теория о целесообразном пределе точности при измерениях. Она указывает те пределы, в которых полученные результаты имеют реальное значение. Эти пределы зависят от относительной величины ошибок, неизбежных при измерении. Эта теория указывает так называемые „значащие цифры“, которые выражают действительные результаты измерения.
Исходя из всех высказанных здесь соображений, мы не можем согласиться с Хэмбиджем, когда он утверждает, что нашел способ, при помощи которого греческие зодчие определяли архитектурные пропорции.
Однако это не мешает книге быть полезной для архитектора обилием собранного в ней интересного фактического материала.
ВВЕДЕНИЕ
Симметрия* служит ритмической основой рисунка. Невозможно ввести в композицию рисунка ритм, не введя предварительно симметрии. Известная доля симметрии и ритма имеется в каждом рисунке, но только лучшие содержат их в достаточной мере. Слабость рисунка зависит от бедности симметрии и ритма.
____________
* В отличие от общепринятого у нас значения слова „симметрия“ автор вкладывает в этот термин то содержание, которое он имел у греков, понимая под словом „симметрия“ соразмерность художественных форм и частей художественного произведения. Прим. ред.
История рисунка показывает нам с несомненностью, что подлинные мастера композиции применяют симметрию и ритм сознательно. Если художник не понимает симметрии и ритма, то он может рисовать только вслепую, доверяясь своему чутью. Так и должно быть, но только до известной ступени развития художника. Между тем эта ступень скоро достигается, и если у художника нет ничего, кроме чутья и склонности на него полагаться, то он останавливается в своем развитии; дальше ему приходится итти ощупью за недостатком технических знаний, которые необходимы для преодоления даже простейших трудностей. Его зрительные художественные способности суживаются, а достижения умаляются, если он не понимает, как построить свои образы, чтобы достичь композиционной силы.
Художники прошлого добивались симметрии и ритма в своих композициях различными методами, но лучшим из всех является тот, который применяли мастера рисунка классического периода искусства древней Греции.
Принципы, которыми руководились эти мастера, были утеряны свыше двух тысяч лет тому назад; теперь они найдены вновь; эти принципы изложены в настоящей книге.
ОГЛАВЛЕНИЕ
Предисловие ... 5
Введение ... 11
Часть первая
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ДИНАМИЧЕСКОЙ СИММЕТРИИ
Глава 1. Симметрия, ее статический и динамический аспекты ... 15
Глава 2. Динамические ряды геометрических фигур ... 27
Глава 3. Динамическая симметрия и закон распределения листвы ... 40
Глава 4. Греческая чаша, как пример композиции, основанной на прямоугольнике
 ... 54 ... 54
Глава 5. Построение композиционных схем ... 63
Глава 6. Греческий метод анализа площадей ... 71
Глава 7. Прямоугольники как художественно-композиционные темы ... 77
Глава 8. Кресло как пример динамической композиции ... 84
Глава 9. Архитектурные украшения ... 92
Глава 10. Оформление книг и набора ... 98
Глава 11. Композиционное построение ... 104
Глава 12. Спирали ... 110
Часть вторая
ДИНАМИЧЕСКАЯ СИММЕТРИЯ ПАРФЕНОНА И ДРУГИХ ГРЕЧЕСКИХ ХРАМОВ
Глава 1. Метод анализа здания ... 119
Глава 2. Фасад и его подразделения ... 126
Глава 3. Антаблемент ... 132
Глава 4. Колонна Парфенона ... 139
Глава 5. Пол храма ... 149
Глава 6. Пол храма и стены здания ... 155
Глава 7. Панафинейский фриз и целла ... 160
Глава 8. Наос ... 163
Глава 9. Антефикс ... 167
Глава 10. Греческая спираль ... 176
Глава 11. Второй храм, построенный архитектором Парфенона ... 186
Глава 12. Дорийские храмы на острове Эгине и в Олимпии ... 191
Примечания ... 197
Примеры страниц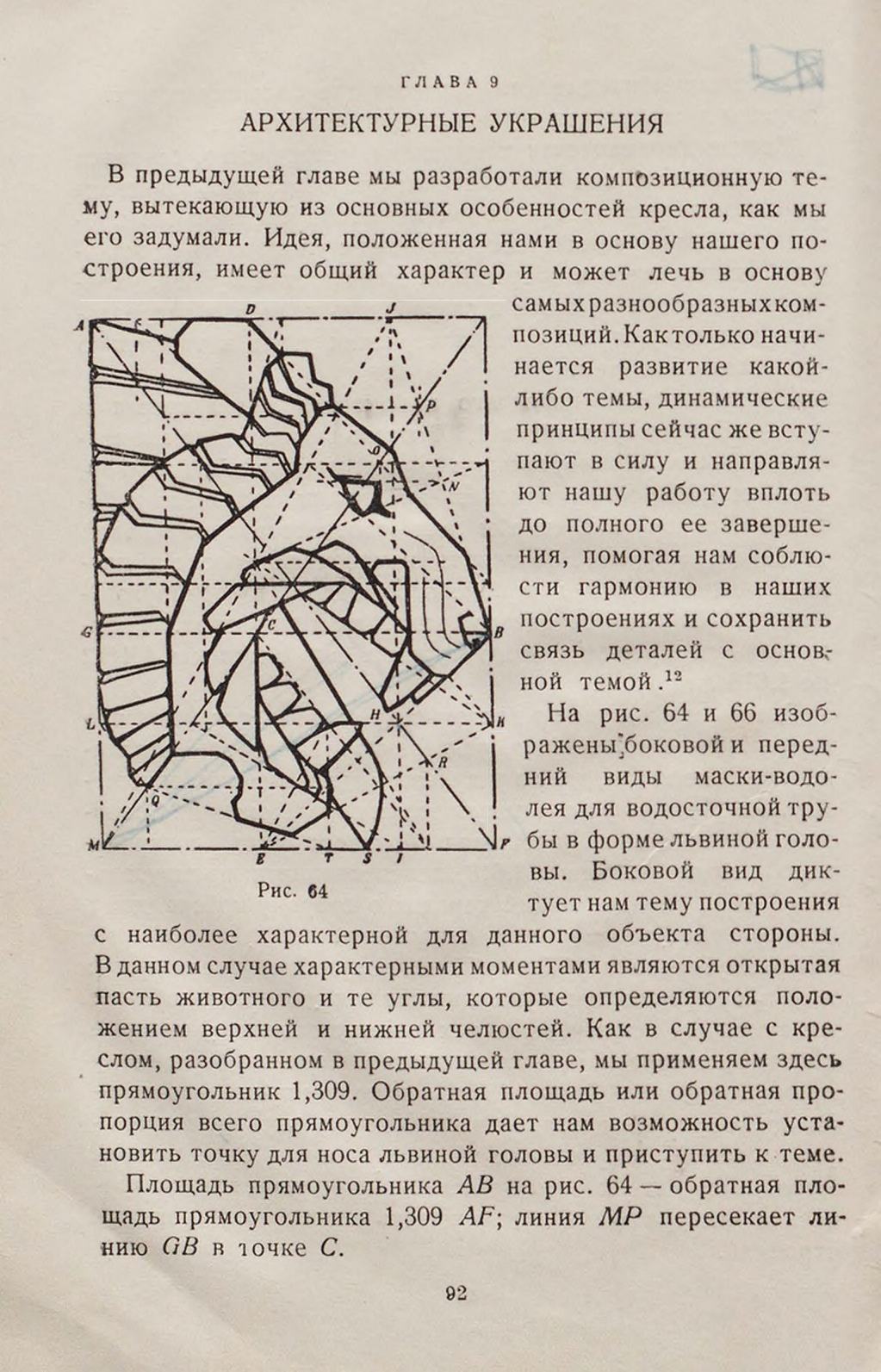 
Скачать издание в формате pdf (яндексдиск; 41,2 МБ)
30 марта 2024, 14:23
0 комментариев
|
Партнёры
|






Комментарии
Добавить комментарий