|
|
Л. Павлов. Гармонизация архитектуры
Le Modulor. Image Courtesy of Centre Pompidou / Dist. RMN-GP/ Ph. Migeat; © FLC, ADAGP, Paris 2015
Публикуем статью архитектора Л. Павлова о формировании образа в архитектуре через гармонизацию целого и отдельных частей здания. Особое внимание в проблеме гармонизации архитектурного сооружения уделяется принципу золотого сечения, породившему модулор Ле Корбюзье и систему пропорционирования И. В. Жолтовского. Иллюстрации добавлены нами (TEHNE), в оригинальной публикации какие-либо иллюстрации отсутствуют.
Павлов Л. Гармонизация архитектуры // Вопросы теории архитектуры (тезисы лекций для семинаров повышения квалификации архитекторов) : Сборник статей / Редакционная коллегия: К. А. Держинский, Ж. С. Розенбаум, А. В. Рябушин ; Союз архитекторов СССР. — Москва, 1976. — 135 с., ил. — С. 40—50.ГАРМОНИЗАЦИЯ АРХИТЕКТУРЫЛ. Павлов
Архитектура, формируемая как среда, в которой существует человек, оказывает влияние на характер общественных отношений, то есть является активным социальным фактором.
Архитектурные сооружения, выполняя определенные функции, удовлетворяют потребности производства, быта, культуры, отдыха. Эти функции необычайно быстро изменяются, соответствуя новым потребностям, и сооружения быстро становятся непригодными для удовлетворения новых функций.
Учитывая фактор времени, архитектура должна стремиться к форме, способствующей развитию усложняющейся функции.
Развитие строительной техники идет очень быстро, быстро развиваются масштабы строительства, изменяются строительные материалы, усложняется техническое оснащение сооружений, здания становятся машинами для производства жилья, отдыха, культуры. Отдельные технические условия эксплуатации зданий сталкиваются друг с другом и входят в противоречие с частями и целым.
Находясь в прямой связи с уровнем строительного искусства и строительной техники архитектура обобщает все достижения в этой области. Архитектурное сооружение должно формироваться на самом высоком уровне современных строительных возможностей с использованием самого совершенного оборудования и с потенциальной возможностью внедрения всех новых достижений техники.
Архитектура — искусство самого массового и самого непосредственного воздействия на человека. С раннего детства и до поздней старости человек испытывает на себе эстетическое влияние той архитектурной среды, в которой проходит его жизнь. Художественные качества являются основным неотъемлемым достоинством архитектуры-искусства и влияние ее на человеческое сознание безгранично.
Все основные признаки, формирующие архитектуру, испытывают страшный натиск времени.
Быстро меняются формы социального заказа, изменяются общественные отношения, порождая новые перспективы формирования будущего.
Быстро меняются способы производства, характер функциональных связей, формы человеческого бытия и оснащение быта, изменяются и расширяются человеческие потребности.
Быстро меняется строительная техника, невозможное делается возможным, уникальное — привычно обыденным.
Архитектор, получая социальный заказ, должен смотреть вперед, философски осознать опережение времени, чтобы продлить функциональную необходимость сооружения. Строя функциональную систему, архитектор должен постичь такую степень обобщения функции, чтобы получить сооружение, рассчитанное на подвижную функцию. Испытывая огромное давление строительной индустрии, ее роста, ее глубоких сдвигов, архитектор должен найти наиболее прогрессивный тип возведения здания и оснастить его совершенным оборудованием, чтобы жизнь сооружения была долговечна.
Но для того, чтобы материальные затраты были наиболее эффективны, архитектор должен создать сооружение бессмертным и бесконечно полезным человеку. Ведь время щадит только эстетические качества архитектуры; только здание, обладающее художественными достоинствами, способно пережить все претензии, которые время предъявляет к сооружениям. И когда здание перестает отвечать социальному заказу, перестает выполнять свои изначальные функции, когда его строительные конструкции и техническое оснащение уже не отвечают требованиям времени, это здание, если оно имеет эстетические качества, становится памятником архитектуры, и именно эстетические качества делают его ценным для воспитания человеческих душ, для создания потенциала художественных представлений, способных формировать новые произведения искусства.
Сегодня труд архитектора бесконечно сложен, потому что современное здание оснащается десятками технических систем, такими, как отопление, кондиционирование, электроснабжение, телефон, радио, газификация, телевидение, водопровод, канализация и многие другие. Ни дворцы Ренессанса, ни петербургские дворцы — ничего похожего не имели, и весь опыт и весь труд зодчего был сосредоточен тогда на создании прекрасного образа.
И неужели ныне, полностью отдав себя решению социальных, функциональных и строительно-технических проблем, потонув в тысяче сложных вопросов, противоречивых и дополняющих друг друга, временных и вечных, больших и частных, архитектор должен отказаться от работы над художественным образом сооружения?
Думаю, что современный архитектор должен так организовать свои груд, чтобы большую половину своего времени посвятить решению таких задач, как гармонизация, поиски общего и частного в их взаимосвязи, пропорционирование — то есть всему тому, что может выразить его внутренний художественный потенциал, всему тому, из чего создается произведение архитектуры.
Художественный образ может быть творческий. Образ может быть и «потребительский», как результат процесса восприятия.
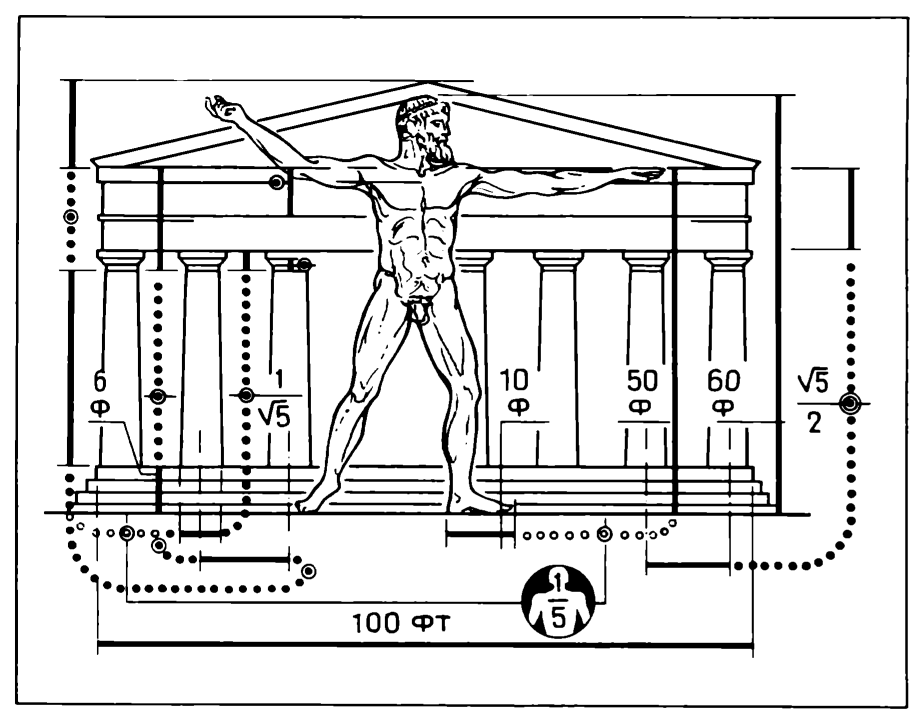
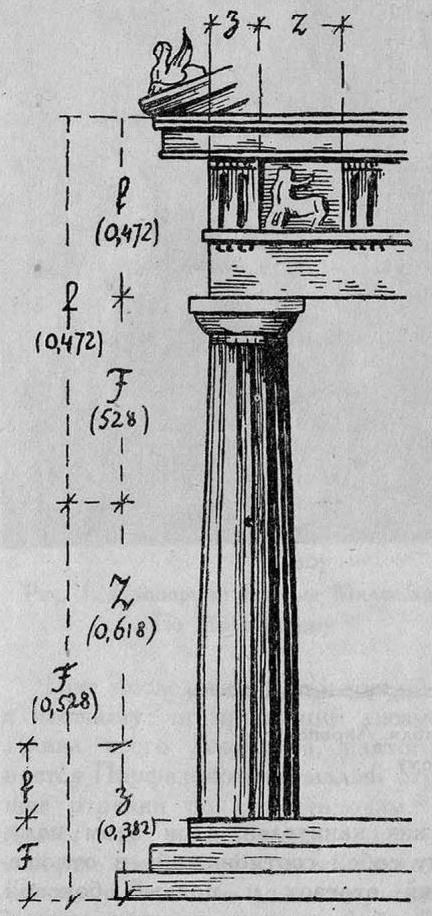
Замысел Парфенона показывает, что числа 10 и 100 для античного грека — те же единицы, но высшего порядка. Из работы Иосифа Шевелева «О формообразовании в природе и в искусстве» (Золотое сечение : Три взгляда на природу гармонии / И. Ш. Шевелев, М. А. Марутаев, И. П. Шмелев. — Москва : Стройиздат, 1990).
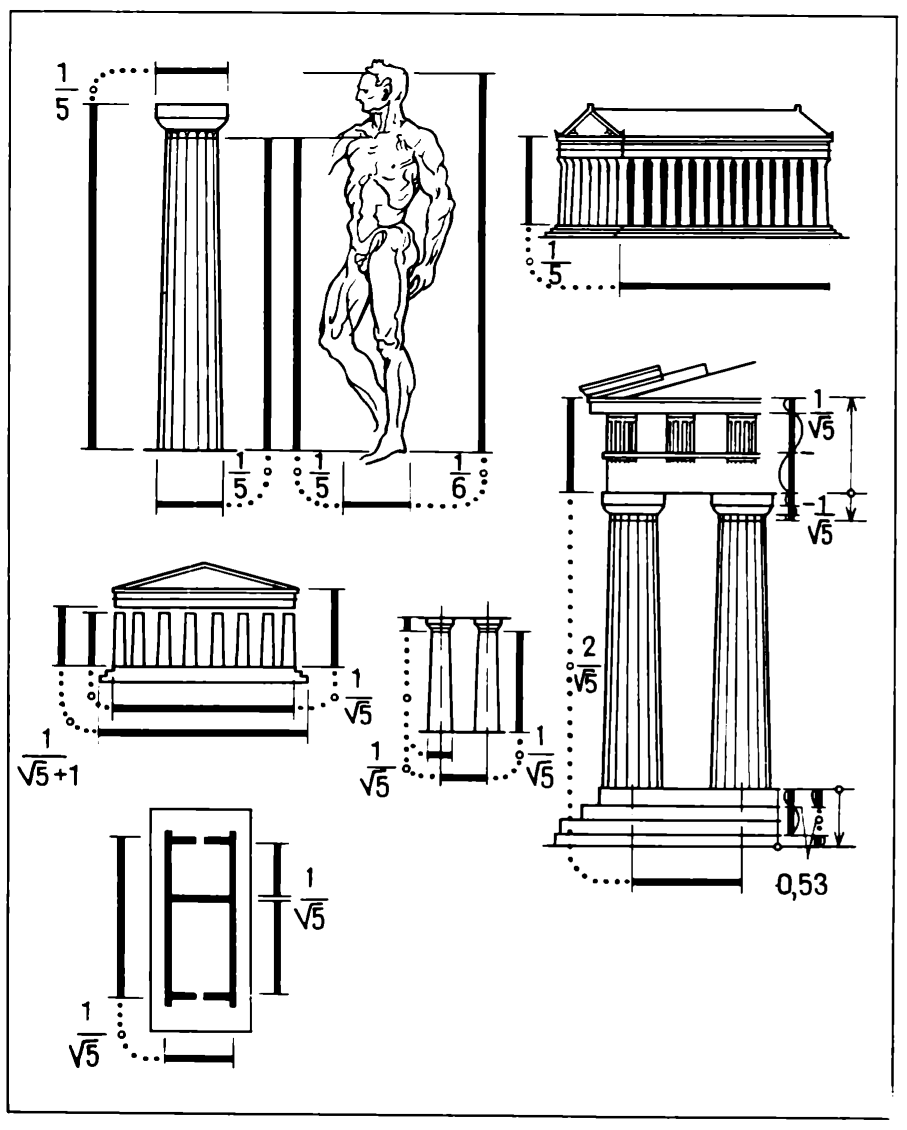
Парфенон. Соразмерность колонны и храма в целом 1:5 и пропорция 1:√5 ассоциируют обнаженное мужское тело — идеал стройности, силы, гармонии. Из работы Иосифа Шевелева «О формообразовании в природе и в искусстве» (Золотое сечение : Три взгляда на природу гармонии / И. Ш. Шевелев, М. А. Марутаев, И. П. Шмелев. — Москва : Стройиздат, 1990).
Творческий потенциал художника способен пробудить творческий потенциал зрителя для завершения всего процесса действия художественного произведения по такой цепи: архитектор-художник — творческий образ — произведение архитектуры — образ, складывающийся в восприятии зрителя.
Если творческий процесс не доходит до конца и образ восприятия совпадает с образом творческим, мы имеем ремесло, то есть ту деятельность, которая не выражает индивидуальности художника и зрителя, не отражает их различия, основывается на пассивности процесса воздействия.
Творчество архитектора-художника должно быть глубже, богаче, потенциально умнее и сложнее общих представлений об искусстве. Он не должен стремиться раскрыть себя сразу, а должен заинтересовать зрителя, «запутать» его, заставить самого искать разгадку, чтобы возбудить творческую активность зрителя в постижении сути своего произведения. «Сначала надо сделать все просто, а потом немножко попутать», — говорил И. В. Жолтовский.
Построение образа не должно исходить из одной схемы мышления, а должно отразить в себе столкновение двух или нескольких систем, может быть даже противоречивых.
Образ может рождаться из аллегорий и тогда схема создания образа будет такая: аллегория — понятие — образ. Пути для раскрытия такого образа слишком прямы, и ключи от него вручаются зрителю сразу, с самого начала.
Образ может рождаться из символа, и тогда схема будет такая: символ — идея — образ. В этом случае символ не имеет прямого раскрытия и прямых аналогий, он всегда нов и неповторим, он отныне будет связан только с этим произведением архитектуры и восприятие этого образа может способствовать рождению тысяч аллегорий, то есть появляется прямой путь к множественности образа восприятия.
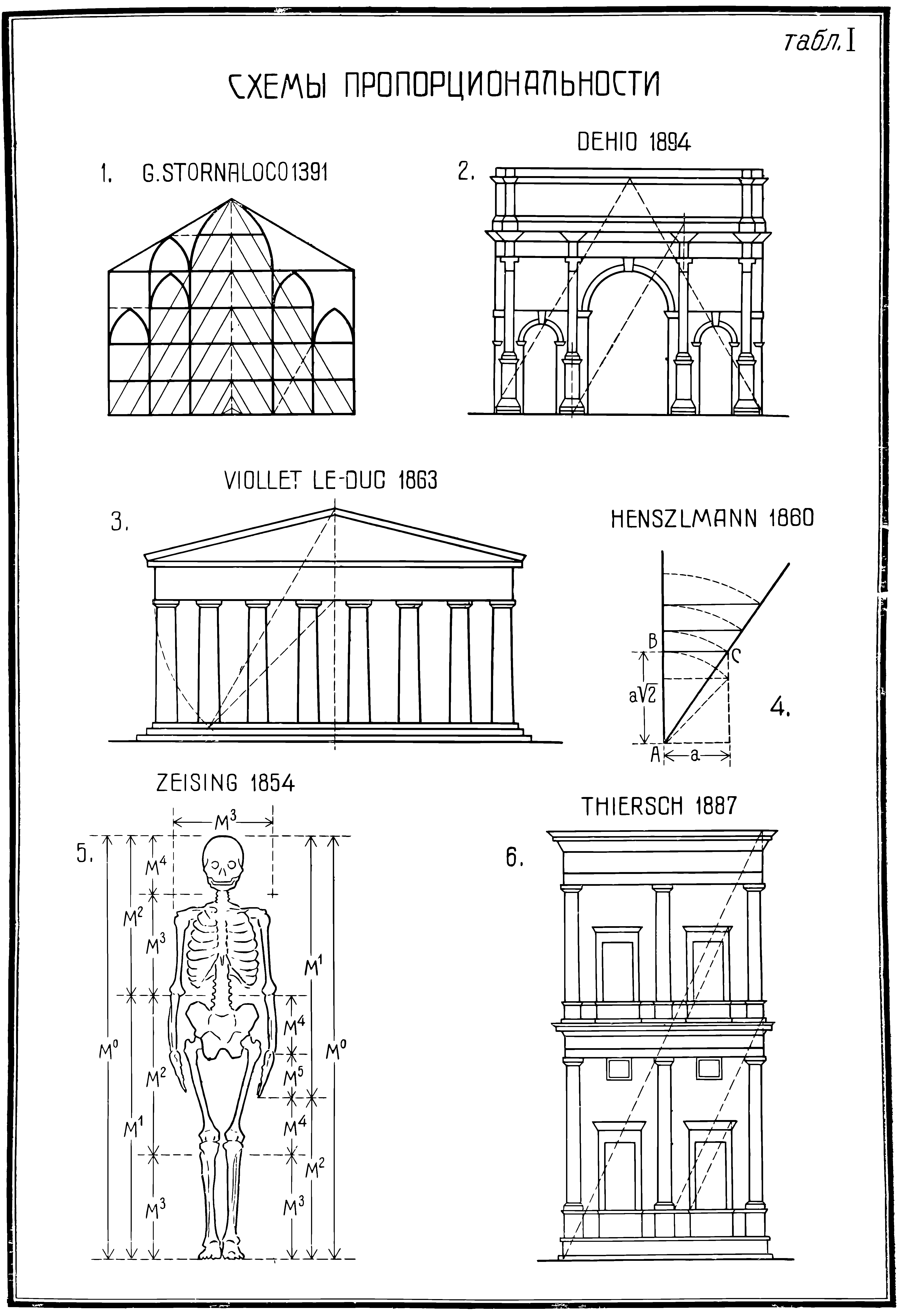
Схемы пропорциональности из издания Пропорциональность в архитектуре / проф. Г. Д. Гримм. — Ленинград ; Москва : ОНТИ, Главная редакция строительной литературы, 1935.
Но насколько труднее этот путь, путь создания символа, путь отказа от прямого использования аллегорий. Приняв, отыскав определенный символ, создав идею сооружения, архитектор приступает к разработке темы, он как бы передает ее разным инструментам оркестра, изменяет ее звучание, раскрывает разные стороны этой темы и в конечном результате устанавливает момент возникновения второй темы — анти-темы, вступающей в борьбу с основной темой, определив, какую силу она должна приобрести, чтобы ее звучание не разрушило основную тему.
Все это удивительно интересный и необычайно сложный процесс на пути формирования образа. Его разработка и углубление переходит и гармонизацию целого и отдельных частей здания. Единство, контрастность, борьба, слитность, темп, ритмы, метры, пропорции, плотность, каркасность, массивность — сколько совершенно различных приемов, которые дают возможность архитектору выразить свою идею в строительной структуре здания. Сознательное оперирование этими категориями, точность окончательно выбранных приемов, точность пропорциональных построений, создание единой пропорциональной схемы, нарушение этой схемы для создания главного, основного в сооружении, того, что не подчиняется общим законам — все это открывает огромные возможности для формирования образа.
Огромные возможности в построении архитектурного образа дает скульптурная масса самого сооружения, лепка объема, исследование соотношения оболочки и каркаса-скелета. Грузность и легкость архитектурной композиции, открытость и скрытость структуры, наконец, изобразительность структуры — все эти приемы правомерны при создании образа.
В архитектуре большое значение имеет пространство, его размеры, пропорции и, наконец, трактовка.
В проблеме гармонизации архитектурного сооружения особое положение занимает «золотое сечение». Вокруг «золотого сечения», его применения и теории всегда шли большие споры, возникали бесконечные толкования. Принцип золотого сечения породил модулер Ле Корбюзье, систему пропорционирования И. В. Жолтовского.
Архитектор Рафаэль Араухо «Раковина моллюска Наутилус помпилиус»

Схема «Пропорциональность спирали» из издания Пропорциональность в архитектуре / проф. Г. Д. Гримм. — Ленинград ; Москва : ОНТИ, Главная редакция строительной литературы, 1935.
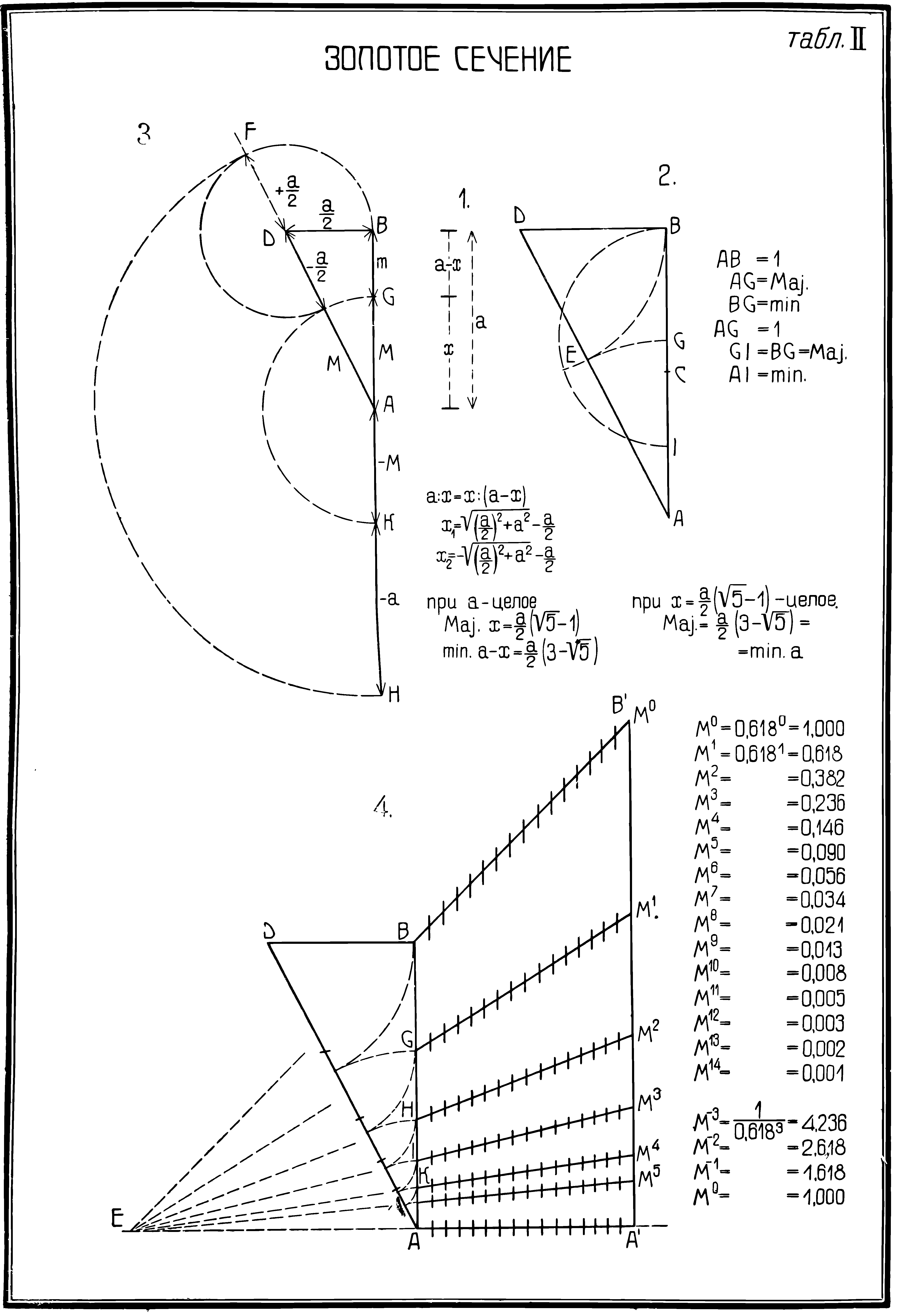
Схема «Золотое сечение» из издания Пропорциональность в архитектуре / проф. Г. Д. Гримм. — Ленинград ; Москва : ОНТИ, Главная редакция строительной литературы, 1935.
В теоретических работах Хембиджа, Месселя, Гика, Гримма и других архитекторов и исследователей глубоко и всесторонне разработаны вопросы развертывания золотого сечения в ряды, геометрического построения золотого сечения, отыскания золотого сечения в природе, растениях, раковинах, животных, человеке.
Вопросам золотого сечения посвящена огромная литература. Начиная с эпохи Ренессанса об этом написано много книг и очень трудно высказать новую точку зрения. Однако, мне кажется, что такая необходимость назрела, потому что философская сущность самого золотого сечения, его математическое достоинство и его исключительность требуют защиты от превращения золотого сечения в одну из множества пропорциональных систем, разворачивающихся в бесконечный ряд.
В чем сущность золотого сечения? Для того, чтобы понять ее, потребуется разобраться в эстетической сущности гармонизации архитектурных сооружений.
Любое отношение двух величин может быть одинаково красивым и безобразным, пока их не связывает никакая математическая и эстетическая закономерность.
Когда появляется закономерность, и отношения разворачиваются з ряд, мы имеем дело с пропорциями. Пропорции бывают арифметические, геометрические и гармонические, в арифметических пропорциях имеется постоянное слагаемое, в геометрических — постоянный множитель, в гармонических множитель развивается с развитием пропорции. Литературные источники Ренессанса предлагают нам много разных рядов пропорциональных отношений, причем наиболее многообразными являются ряды гармонических пропорций. Анализ сооружений Ренессанса показывает, что мастера архитектуры этой эпохи не только писали о гармонических пропорциях, но и применяли в своих постройках преимущественно гармонические пропорции.
Если золотое сечение развернуть в ряд, оно займет место среди геометрических пропорций, станет одной из многих возможных шкал гармоничных отношений, бесконечно повторяющихся в пропорциональном ряду. Но почему же именно золотое сечение так волнует мастеров зодчества на протяжении всей истории архитектуры?1
Мастера классической архитектуры стремились к художественному единству архитектурного организма, к его завершенности, обусловленной соподчиненностью целого и его частей. Именно это стремление связать в единую гармоническую систему целое и отдельные части целого привело архитекторов к золотому сечению. В самом названии пропорции заложена вся глубокая философия этого творческого метода. Целое рассекается на две части так, что большая часть относится к целому как меньшая часть к большей части. Мы видим прямую связь целого и его частей.
Это первое и самое главное свойство золотого сечения при разворачивании его в пропорциональный ряд полностью утрачивается, причем то, что целое есть сумма двух частей создает в ряду ряд дублей т. е. повтор одинаковых величин. На этом свойстве построены ряды Фибоначчи, которые выражены в целых числах, спиралью вьются вокруг прямой золотого отношения, постепенно затухая, асимптотически приближаясь в бесконечности к прямой, давая приближенные, выраженные в целых числах значения золотого сечения.
Это параллельно возникающее мертвое равенство, уничтожающее ощущение роста, заставило мастеров Ренессанса отказаться от применения золотого сечения в трехчастных ренессансных фасадах. Формула золотого сечения, соединяя в себе отношение и пропорцию, создает равенство отношений.
При золотом сечении отрезка получается единственно возможное математически отношение, которое при включении целого в формулу пропорции разворачивается в бесконечный ряд. Пропорции — это второе неповторимое свойство золотого сечения, оно порождено первым свойством и способно его разрушить.
Третьим основным свойством золотого сечения является сопровождение основного ряда золотых отношений рядом накладывающихся друг на друга парных равенств, каждый из членов которых находится в золотом отношении с предыдущими и последующими членами первых равенств.
При развитии в ряд золотое сечение быстро подходит к своему экстремальному завершению, причем развитие ряда частей целого завершается там, где целое получает дополнительное членение, равное большей части, то есть тогда, когда целое становится частью нового, вновь родившегося целого. Таким образом целое является пределом ряда, построенного на меньшей части целого. Это удивительное свойство снова соединять части и целое в единую гармоническую систему и является четвертым основным свойством золотого сечения.
Все четыре свойства тесно переплетаются, входят в противоречие друг с другом, но неизменно образуют ту неповторимую основу для гармонизации архитектурных сооружений, которая должна исходить из использования всех этих удивительных свойств, не превращая золотое сечение в обычную геометрическую пропорцию.
У нас на Руси издавна мерили все человеком с поднятой рукой — саженью, равной 2 метрам 13 сантиметрам (до сих пор, когда мы плаваем, выкидывая вперед руку, этот стиль называется «саженки»). Русская сажень соответствовала человеку с ростом 172 сантиметра, она делится на три аршина. Принятая на Руси четырехаршинная высота жилых горниц, изб соответствовала 284 сантиметрам, на высоте сажени делались полки, на которые в северных избах ставилась вся утварь. На высоте 42 сантиметров делались лавки, на которых сидели и спали. Вся эта система измерения близка к модулеру Корбюзье. Вот почему для нас, русских архитекторов, ознакомление с модулером Корбюзье представляет огромный интерес, а объективный анализ его системы измерений может дать много интересных выводов.
Мне запомнились две встречи с Корбюзье в Москве. Одна произошла в Юшковой доме на Мясницкой улице, где помещался архитектурный факультет Вхутемаса. В круглом зале собрались студенты мастерской А. А. Веснина, и вот вошел Корбюзье — среднего роста, суховатый, в сильно поношенном демисезонном пальто, в котелке, с тросточкой. Он снял котелок, положил его на стол, бросил в него перчатки, и мы увидели человека с туго натянутыми назад волосами, с ничем не примечательной внешностью, в тяжелых очках, которые он все время приподнимал правой рукой. Корбюзье показывали студенческие работы, причем А. А. Веснин, стеснительный, извиняющийся, делал попытки переводить с русского на французский и обратно. Трудно было вести беседу, но все же на нас произвел огромное впечатление острый сильный ум этого архитектора, живописца, скульптора, математика, философа, публициста — человека, ускользнувшего от влияния академического духа, сохранившего ясную голову, способность воспринимать новое.
Вторая встреча произошла в зале Академии художеств. Там Корбюзье прочел лекцию, в которой излагал основные принципы своего понимания современной архитектуры.
На больших листах бумаги он рисовал схемы построения современной конструкции здания и схемы гармонизации и пропорционирования. Листы, снятые с мольберта, развешивались на веревке при помощи щипцов, и этот способ экспозиции давал возможность легко возвращаться к каждому рисунку в нужный момент.
Нам было ясно, что мы имели дело с человеком могучего творческого темперамента, который нашел выражение для передачи всей глубины своих концепций, осмыслив их как стройную философскую систему. «Архитектура, скульптура, живопись находятся в прямой зависимости от пространства, будучи связаны необходимостью управлять им каждая с помощью соответствующих средств. Существенно важно отметить, что ключом к эстетической эмоции служит пространственная функция».
Искусство тем отличается от науки, что оно руководствуется не законами, а закономерностями, выбор которых невольно принадлежит автору. Корбюзье занимался гармонизацией и поисками модулера, способного переложить искусство на язык математики. Он писал: «Природа — это действительно математика». Шедевры искусства созвучны природе, выражают ее законы. А отсюда произведения искусства есть тоже математика, и исследователь вполне может применять к произведению искусства ее беспощадные умозаключения и неумолимые формулы. Однако Корбюзье говорит: «Но во всех случаях я оставляю за собой право сомневаться в бесспорности решений, подсказанных мне модулером, сохраняю полную свободу действий, подчиняя их моему чувству вещей, но отнюдь не моему разуму».
В сущности всякая деятельность есть искусство, если среди закономерностей еще не сформировались законы. Так, математика для греков вначале была искусством, искусством она остается и в наше время на вершине своего становления, где среди закономерностей идет дальнейший поиск новых законов.
Поиски эстетических закономерностей велись греками, римлянами, мастерами готики, Ренессанса, русскими мастерами и современными архитекторами.
Греки применяли вращающиеся прямоугольники, параллелепипеды, используя священное число Пифагора √5 = 2,236.
Римляне перешли на модульную систему, и изучение Витрувия знакомит нас с системой потрясающей математической стройности.
Мастера готики исходили из окружности и, также как греки, они получили стройную систему, но другого плана.
А зодчие Ренессанса применяли наряду с арифметическими и геометрическими пропорциями гармонические, основываясь на том, что отношения членов развиваются, и создается ряд, дающий систему разности отношений, и художник свободен взять ту или иную часть ряда и получить быстро изменяющееся, развивающееся отношение, или отношения очень близких по величине чисел. Это преимущество гармонической пропорции помогло мастерам Ренессанса создавать свои трехчастные и четырехчастные фасады. В трактатах Альберти, Барбаро, Палладио мы найдем эти пропорции.
Мастера Византии и русского зодчества применяли систему «средопупия», вращая веревку вокруг закрепленного на высоте центра.
А Камерон клал на чертеж равносторонний треугольник, гармонируя фасады и планы.
Стройная система золотого сечения и его функций легла в основу всего творчества Ивана Владиславовича Жолтовского.
Поиски эстетических закономерностей сопровождали творчество всех крупных мастеров архитектуры во все эпохи ее расцвета. Выход в свет в 1927 году книги Гика «Эстетика пропорций в природе и искусстве», труды Хембиджа, Месселя и других авторов обострили интерес к изучению пропорциональных систем.
Основами, на которых покоится модулер Корбюзье, является ряд золотого сечения и ряд Фибоначчи.
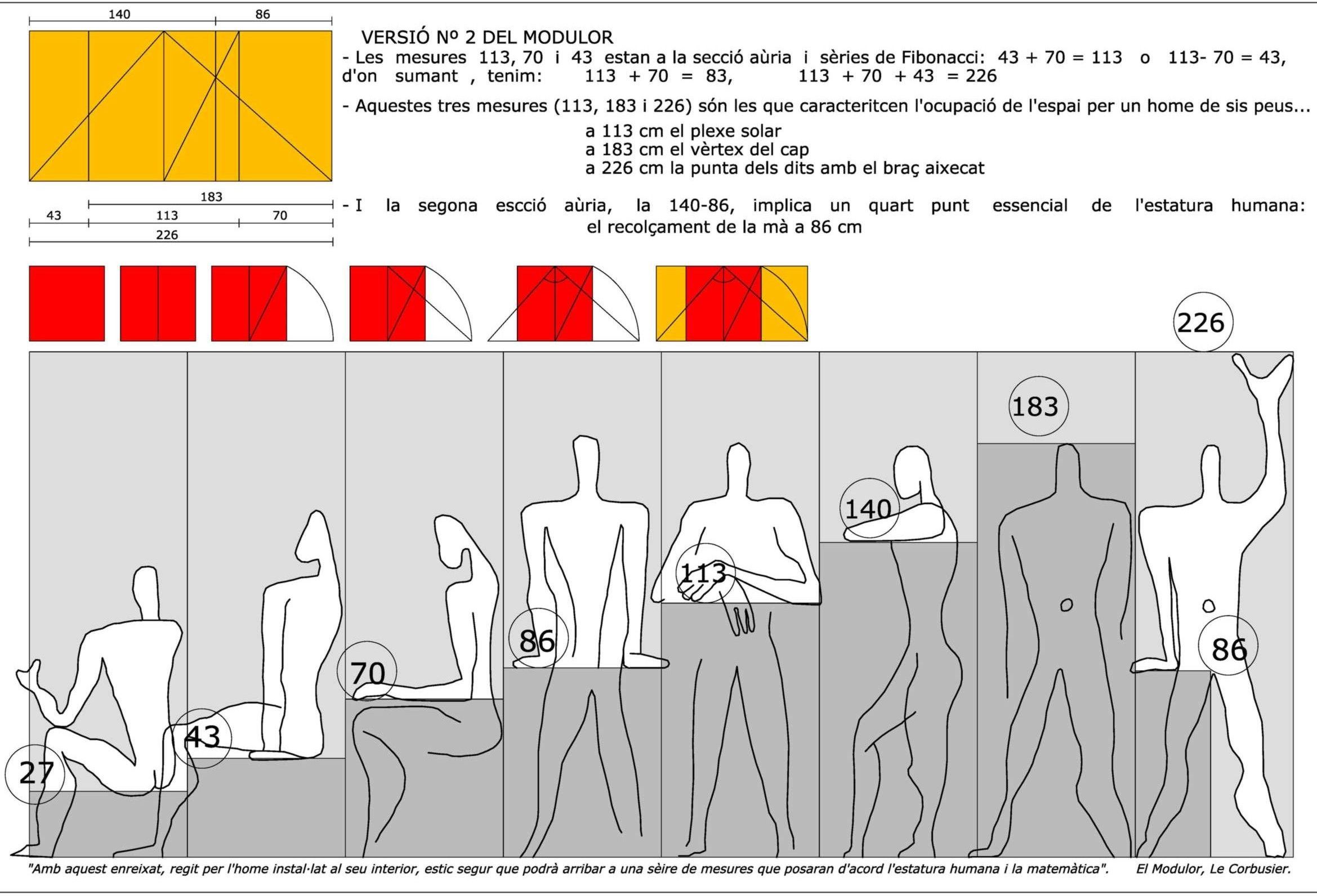 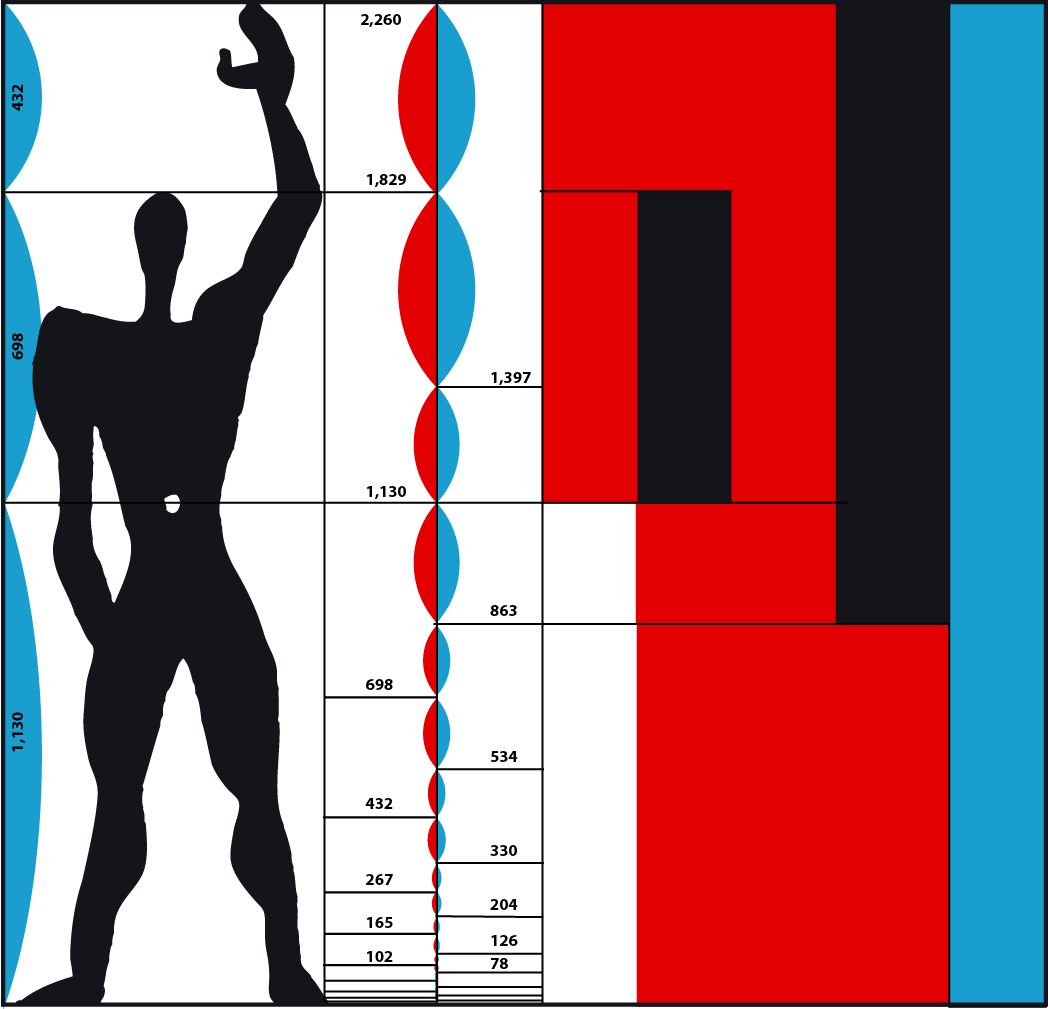
Золотое сечение давно привлекало людей волшебностью своих пропорциональных отношений. Дерево распределяет свои отростки по законам золотого сечения, листики располагаются на ветке по законам золотого сечения. Человеческое тело строится по законам золотого сечения. Если взять за основу человеческих пропорций пуп — место равно удаленное от кончиков пальцев на ногах и руках — то расстояния от земли до пупа и от пупа до верха темени и от темени до поднятой руки будут находится в золотом отношении. Фаланги пальцев руки и фаланги пальцев ноги человека находятся также в золотом отношении, золотой ряд пронизывает все пропорции тела человека, животных, насекомых, растений.
Как уже было сказано, любое отношение двух величин одинаково красиво и одинаково безобразно потому, что оно не содержит закономерности, которая могла бы развернуться в ряд, уходящий к бесконечно малым и бесконечно большим величинам.
Но золотое отношение является единственным, действительно единственным, разворачивающимся в ряд через сумму обоих величин к бесконечно большим и через разность обоих величин к бесконечно малым. В этом математический смысл золотого сечения, однако нельзя не учесть, что золотое сечение несет в своей математической структуре дуализм.
Дуализм золотого ряда дает основание для получения вертикальной и горизонтальной симметрии. Так человек с поднятыми руками делится на две равные части и на три части в золотых отношениях. Этот дуализм обогащает ряды золотых отношений, а иногда мешает правильному прочтению пропорций сооружения.
Ряд, открытый в 1202 г Леонардо Фибоначчи, основан на этом дуализме и при помощи простых числовых значений он приближается к золотому сечению. Ряд Фибоначчи выглядит так: 0—1—1—2—3—5—8—13—21. Если графически изобразить отношения смежных членов этого ряда, то построенная синусоида будет стремиться лечь на линию, изображающую отношения 1 : 1,618. Действительно, отношение первых двух членов равно бесконечности, второй пары — единице, третьей пары — двойке, четвертой — полутора, пятой 1,66 и так далее. Отношения всех четных пар будут немного меньше 1,618, отношения всех нечетных пар больше 1,618.
Ряд Фибоначчи дает возможность, применяя целые числа, находить золотые отношения достаточно точно. (Именно поэтому этот ряд используется дизайнерами при выработке стандартов изделий и установлении благоприятных пропорций).
Для того, чтобы совершенно понять модулер Корбюзье, необходимо вспомнить, что еще в 1928 г. он пришел к идее создания двухъярусной квартиры, перенеся принцип композиции английского дома в современное жилое многоэтажное сооружение. Имея две высоты, одна из которых в два раза больше другой, он должен был в целях экономии объема принять минимальную высоту жилых комнат. В противном случае его система, осуществленная в марсельском жилом комплексе, не выдержала бы экономической конкуренции с одноэтажной, одновысотной квартирой. Именно для марсельского дома и был разработан модулер, и стены этого дома покрыты многократным изображением схемы модулера. Жилой дом в Марселе — 1947—1952 годы, окончательная редакция модулера — 1948 год.
Тщательно разработанная схема модулера имеет два варианта, которые исходят из роста среднего француза и среднего англичанина. Основной идеей модулера является создание сетки размеров, способных точно установить необходимое и достаточное пространство для жизни человека и для оборудования его быта.
Желание мерить архитектуру человеком — давняя традиция строительного дела, такие меры как фут (стопа), локоть, палец, шаг (аршин), человек с поднятой рукой (сажень) сопровождали архитектуру до тех пор, пока не была принята абстрактная мера длины, связанная с размерами земного шара. Принятие метрической системы с десятичной разработкой очень сильно упростило использование размерных построении для создания архитектурных сооружений, но оторвало ее от человека и его размеров.
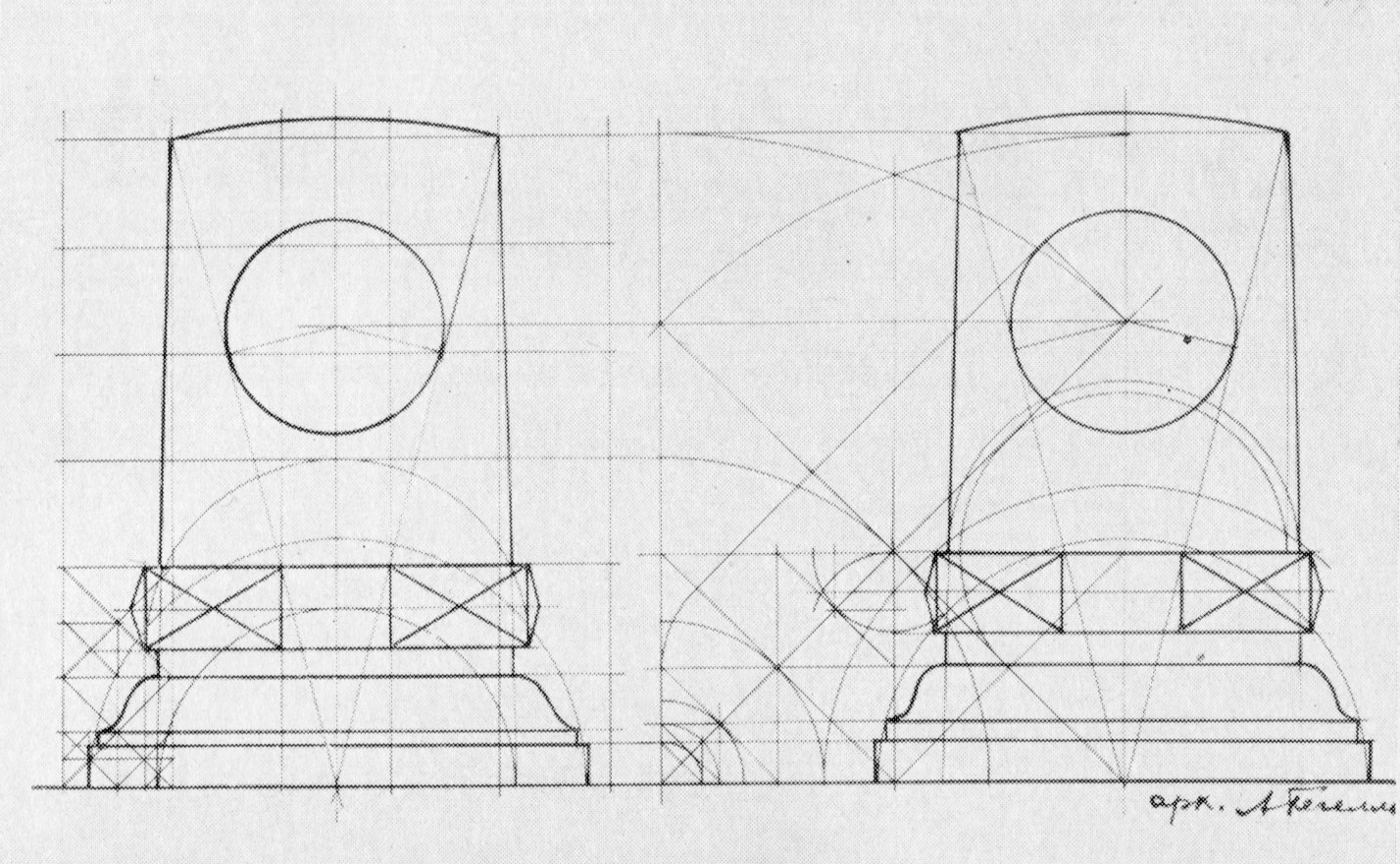
Гегелло А. И. Мемориальная доска-стела крейсера «Аврора» в Ленинграде. Схемы пропорций стелы на основе отношений простых чисел и по канону Поликлета
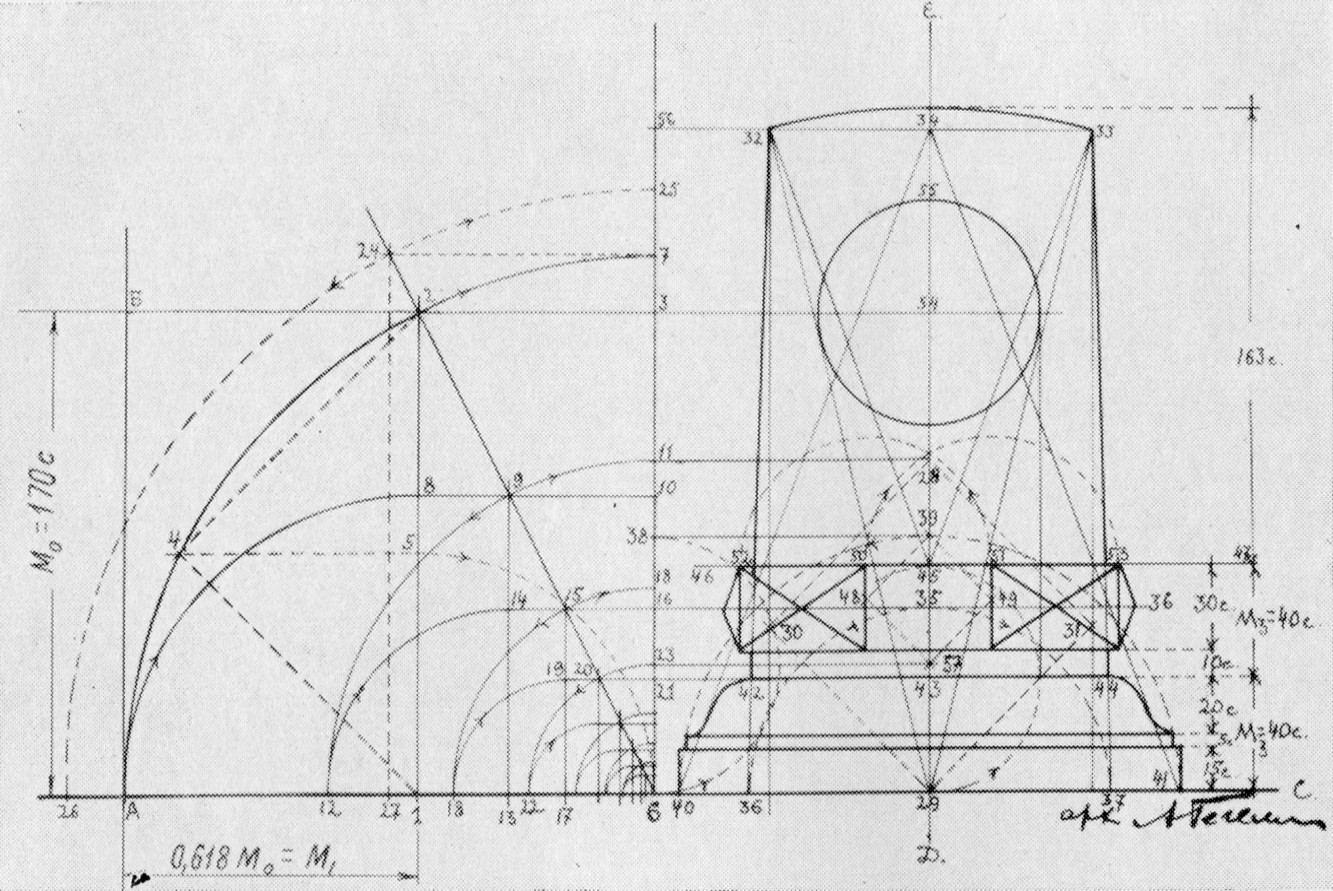
Гегелло А. И. Мемориальная доска-стела крейсера «Аврора» в Ленинграде. Схема пропорций стелы по закону «золотого сечения»
Труден и сложен путь Корбюзье к модулеру. Он исходил из схемы двух квадратов, в которые пытался вложить прямой угол, соскользнувший с середины прямоугольника, и тем самым получить динамический ряд интересных отношений с мягкими пропорциями.
Математически эта схема невозможна, так как прямой угол, вписанный в прямоугольник из двух квадратов, может иметь вершину только на середине большей стороны прямоугольника.
В принятой Корбюзье схеме построение идет от квадрата, разделенного пополам. Из середины основания квадрата берется диагональ половины квадрата и отворачивается до основания, так образуется золотой прямоугольник. Полученная точка соединяется с вершиной, делящей квадрат линией, и в этой вершине строится прямой угол. Пересечение его второй образующей с основанием дает вторую точку, завершающую прямоугольник. Этот прямоугольник Корбюзье без всякого основания объявляет прямоугольником двух квадратов, тогда как отношение его сторон равно 1 : 2,0124. Эта сравнительно малая ошибка не давала Корбюзье обнаружить ее графически, а желание получить динамическую схему было весьма велико.
Хочется вспомнить одно высказывание Татлина: «Если вам нужно соорудить монументальную вещь, берите квадрат плюс один вершок. Квадрат самая устойчивая форма, один вершок придает ему динамичность развития, уводит от безразличного равенства, от смерти к жизни».
Только в последней схеме смирившись с расположением вершин вписанного квадрата на середине прямоугольника, взяв от его сторон отношение золотого сечения Корбюзье удается получить стройную, математически правильную систему золотых отношений с изображением дуализма ряда.
В основной схеме модулера Корбюзье переворачивает развитие ряда вверх ногами и тогда точка, к которой в бесконечности стремится ряд, оказывается на поверхности земли. В этом сказалась целеустремленность автора модулера, желающего доказать закономерность высоты жилых помещений, где человек, подняв руку, касается потолка.
На самом деле, если продолжить ряд «земля-пуп, пуп-темя, темя-поднятая рука» дальше, то этот ряд будет в бесконечности стремится к высоте 2,96 в английском варианте и 2,87 — во французском варианте модулера. А если принять 2,83 (русскую сажень) за русский вариант, то эти логические пределы ряда, строящегося на пропорциях человека, вероятно и будут логическим размером высоты жилых помещений.
 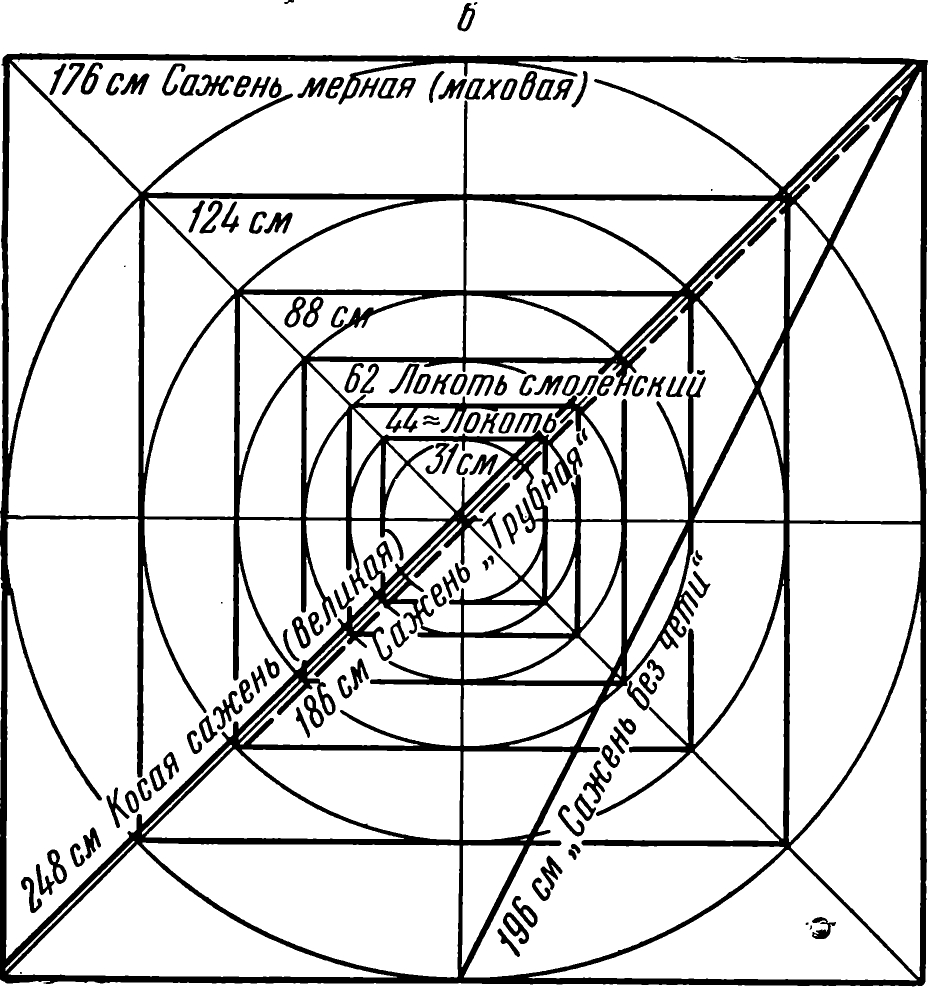
Непонятное для нас одновременное пользование разными мерами длины объясняется заложенными в этих мерах при их создании строгими геометрическими соотношениями. Графическое изображение русских саженей и их долей по принципу «вавилона». Иллюстрации из статьи Б. А. Рыбакова «Архитектурная математика древнерусских зодчих» (Советская археология. — 1957. — № 1).
Если принять такую поправку к модулеру, то отношение роста человека к расстоянию от его темени до потолка будет в золотом отношении, а расстояние от пола до пупа будет равно расстоянию от темени до потолка. Все размеры в такой схеме от крупных, таких как высота помещения и рост человека, до самых малых будут находиться в золотых отношениях.
Модулер Корбюзье несомненно является крупным открытием в разработке антропоморфной архитектурной гармонизации, но он нуждается в доведении до конца, до ясного логического завершения его математической функции. Вероятно это завершение не устраивало самого автора модулера, вероятно оно было ему известно, но отвергнуто как не подтверждающее его личных убеждений. Вот почему это исследование хочется заключить теми же словами мастера: «...во всех случаях я оставляю за собой право сомневаться в бесспорности решений, подсказанных мне модулером, сохраняю полную свободу действий, подчиняя их моему чувству вещей, но отнюдь не моему разуму».

Empreinte du Modulor. Image © FLC, ADAGP, Paris 2015
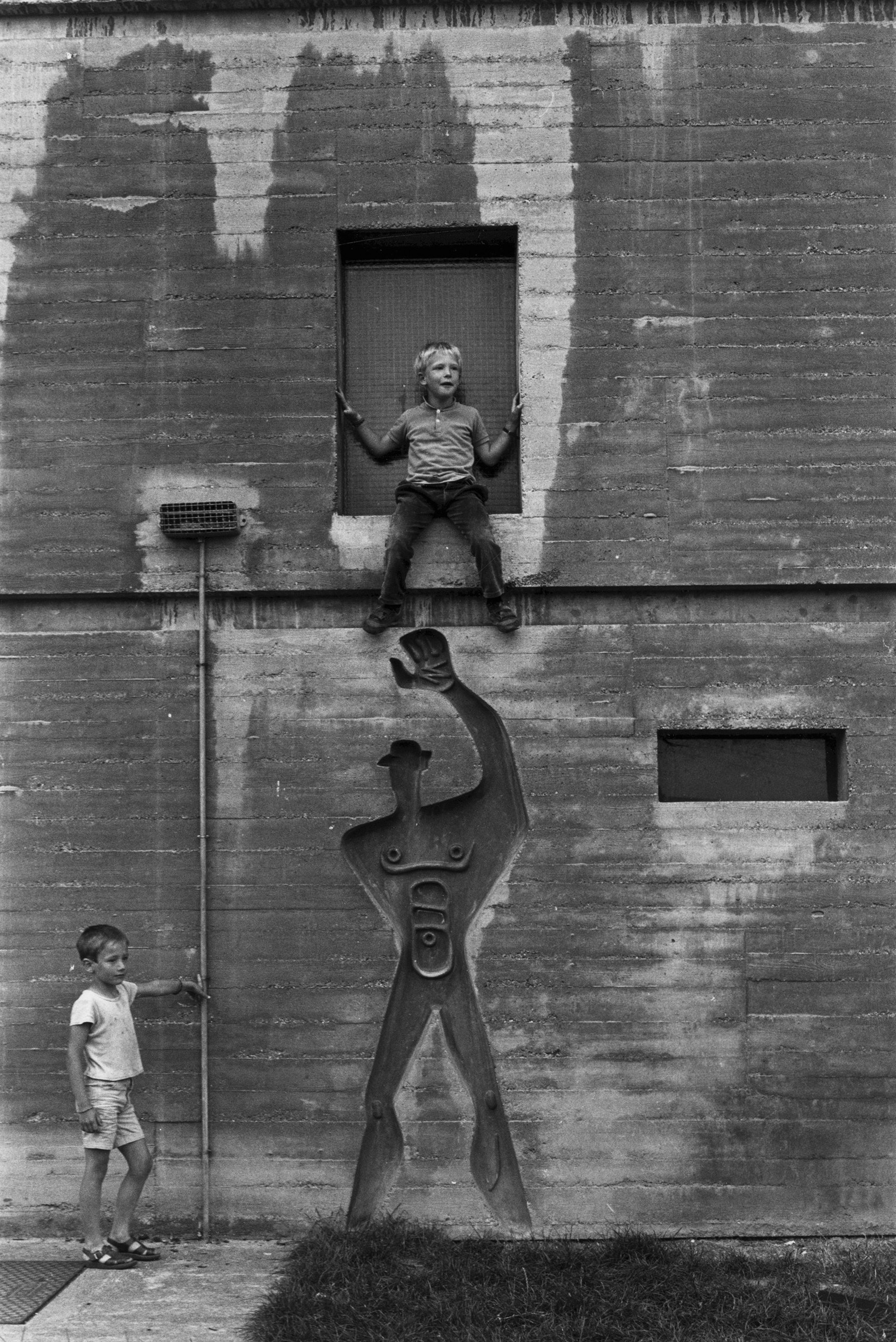
Empreinte du Modulor. Image © FLC, ADAGP, Paris 2015. Source: archdaily.com
Именно когда Корбюзье подошел к открытию закона гармонизации, превращающего архитектуру из искусства в науку, он вновь готов сбросить с себя тяжесть жестких законов, чтобы обратиться к закономерностям, выбор которых подчинен воле художника.
Свобода действий — вот, что вдохновляло этого мастера, неповторимого и всегда неожиданного.
Смело отказываясь от своих убеждений, он шел вперед, подчиняясь своему чувству вещей, далеко опережая время и никогда не повторяясь.
8 марта 2022, 15:14
0 комментариев
|
Партнёры
|
||||||









Комментарии
Добавить комментарий